Recursivité
Un exemple : la fonction Factorielle
La fonction factorielle est définie sur les entiers par $$n!=n\times (n-1)\times ... \times 1$$
le factorielle de n est le produit des n premiers entiers entre eux
Par exemple $4! = 4\times 3\times 2\times 1 = 24$
On peut programmer cette fonction de deux manières:
- itérative à l'aide d'une boucle for
- récursive
Recopiez le programme ci-dessous et testez le pour différentes valeurs 1,3,4, 5 et 17
def factorielleIteratif( n):
produit = 1;
for i in range(1,n+1):
produit *= i
return produit
#----------------------------------
def factorielleRecursif( n):
#Cas de base n = 1
if n == 0 :
return 1
#n! = n * (n-1)!
else:
return n*factorielleRecursif(n-1)
#-------------Programme principal----------------
print("le factorielle de 5 (itératif) est ",factorielleIteratif(5))
print("le factorielle de 5 (récursif) est ",factorielleRecursif(5))
La programmation d'une fonction récursive est basée sur deux idées
Pour un cas de base la fonction retourne une valeur
Pour la fonction factorielle pour n = 0 la fonction retourne 1
Pour la cas général n > 1 dans le corps de la fonction il y a un appel à la fonction elle même mais sur une (ou plusieurs valeurs) valeur inférieure à n
On peut ainsi traduire $n!=n\times (n-1)!$
Exercices
- Construire deux fonctions, l'une itérative et l'autre récursive permettant d'ajouter les n premiers entiers entre eux
- Visualiser la suite des appels récursifs avec Python Tutor. Vous pouvez observer une pile (LIFO) des appels récursifs
- Exécuter la fonction récursive pour n = 992 (pas sur Python Tutor mais dans un IDE) . Vous allez observer que la hauteur de la pile est limitée
Arbre des appels de fonctions
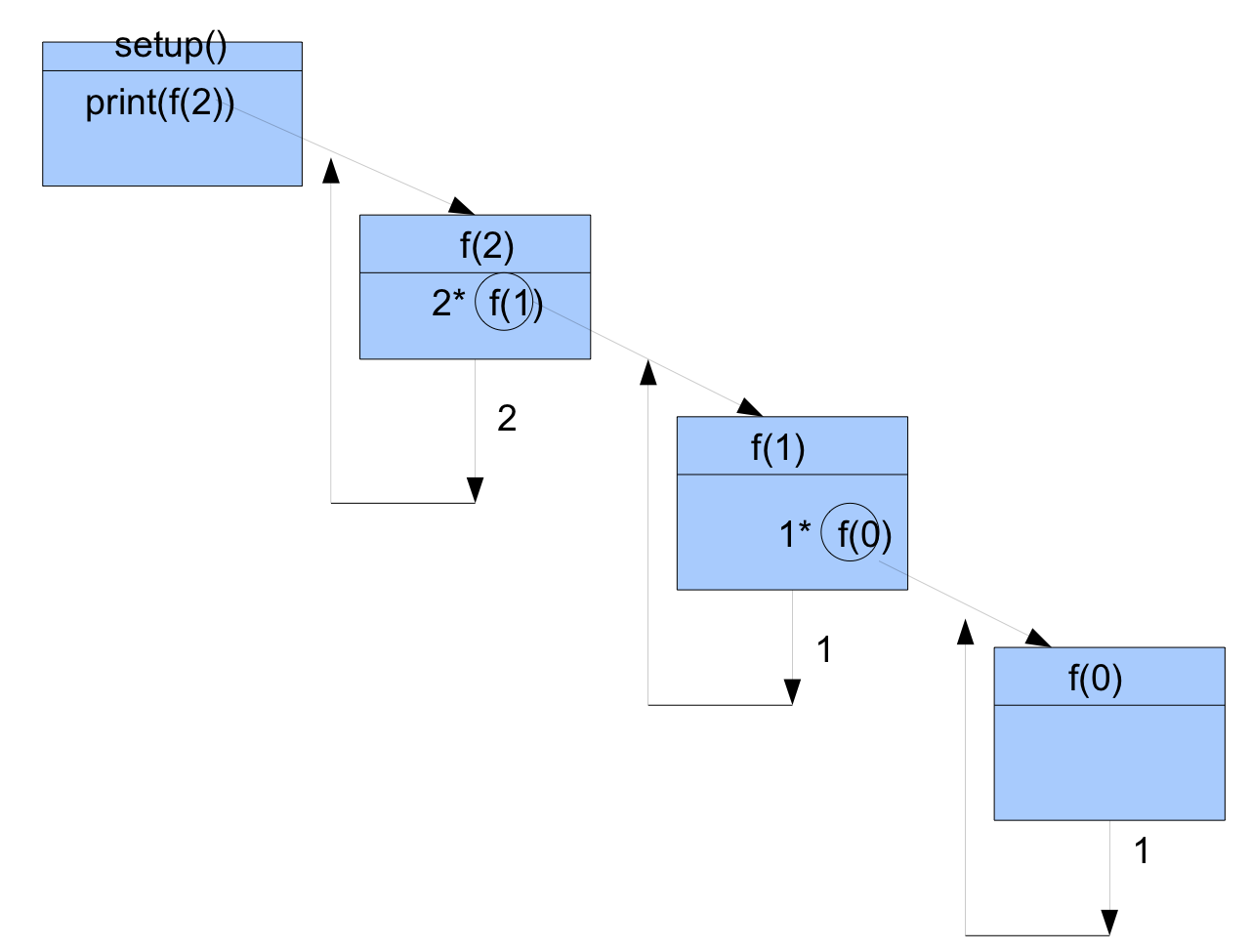
Lorsqu'on appelle la fonction factorielle(2), avant qu'elle n'ait retournée de valeur elle appelle à son tour la fonction factorielle(1) qui à son tour appelle la fonction factorielle(0)
La fonction factorielle(0) retourne la valeur 1 qui prend la place de factorielle(0) dans le corps de factorielle(1) qui va donc se terminer à son tour et retourner 1*1 = 1
Cette valeur 1 va prendre la place de factorielle(1) dans le corps de factorielle(2) qui va donc se terminer en retournant 2*1 = 2
Observer cela sur Python Tutor (le mécanisme des appels récursifs est géré en mémoire par une Pile)
Avantage et inconvénient de la programmation récursive
- Traduction quasiment immédiate d'un algorithme
- La pile des appels récursifs est limité en taille en mémoire, ce qui limite la taille des données. Si on travaille sur des données de grande taille il faudra probablement utiliser un programme itératif. Pour observer cela exécuter factorielleRecursif(1000)
- Appels répétés de la fonction pour les mêmes valeurs (ralentissement du programme)
Regardons cela sur l'exemple de la suite de Fibonnacci:
$u_n =u_{n-1}+u_{n-2}$ avec $u_0=0$ et $u_1=1$
def fibonnacci(n):
#Cas de base n = 1 ou n = 0
print("début de fibonnacci pour n = ",n)
if n == 0 :
print("fin de fibonnacci pour n = ",n)
return 0
elif n == 1:
print("fin de fibonnacci pour n = ",n)
return 1
else:
s = fibonnacci(n-1) + fibonnacci(n-2)
print("fin de fibonnacci pour n = ",n)
return s
print("fin de fibonnacci pour n = ",n)
#-------------Programme principal---------------
print("Fibonnacci de 5 vaut ",fibonnacci(5))
Recopiez et testez le programme ci-dessus
On constate (voir arbre ci-dessous) qu'on appelle plusieurs la fonction fibonnacci pour les mêmes valeurs, par exemple fibonnacci(2) est appelée 3 fois
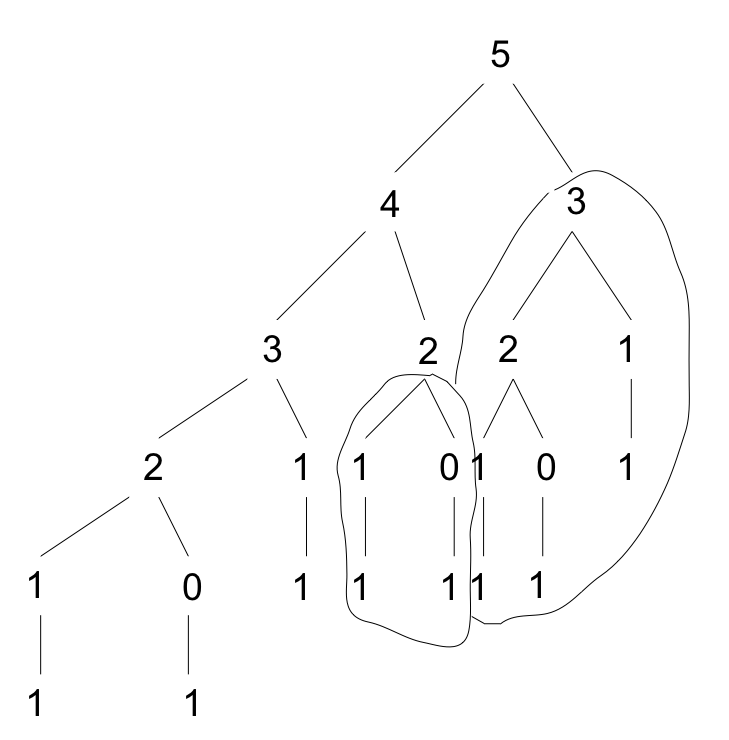
Pour éviter cela on va stocker dans un tableau les valeurs calculées et si une valeur est déjà stockée on retourne cette valeur (mémoïsation)
import time
#------------------Variables Globales--------------
TAILLE_MAX = 50
tableValeurs =[0]*TAILLE_MAX
#------------------Fonctions-----------------------
def fibonnacci(n):
#Cas de base n = 1 ou n = 0
if n == 0 :
return 0
elif n == 1:
return 1
else:
s = fibonnacci(n-1) + fibonnacci(n-2)
return s
#--------------------------------------------------
def fibonnacciMemo(n):
#Cas de base n = 1 ou n = 2
if n == 1 or n == 2 :
return 1
elif(tableValeurs[n] != 0):
return tableValeurs[n]
else:
s = fibonnacciMemo(n-1) + fibonnacciMemo(n-2)
#memoïsation
tableValeurs[n] = s
return s
#-------------Programme principal----------------
debut = time.time()
print("Fibonnacci de 40 vaut avec memoisation",fibonnacciMemo(40))
duree = time.time() - debut
print('Durée en secondes:', duree)
##debut = time.time()
##print("Fibonnacci de 40 vaut sans memoisation",fibonnacci(40))
##duree = time.time() - debut
##
##print('Durée en secondes:', duree)
Recopiez et testez le programme ci-dessus pour calculer la valeur de la suite de Fibonnacci pour n = 20
Comparez les temps d'exécution des deux programmes en utilisant une fonction Python appropriée
Programmation collective
Tours de Hanoï
8 disques sont empilés du plus grand au plus petit autour d'une tige verticale.Il s'agit de les déplacer sur une autre des deux autres tours en utilisant une tour intermédiaire

-
Pour comprendre le problème et trouver la nature récursive de ce problème, essayer avec 3 tours, noter les déplacements des disques et observer bien
De la gauche vers la droite on notera les axes 1,2 et 3 on notera les diamètres arbitraires des disques 6, 5 et 4
Supposons que l'on veuille déplacer les trois disques de l'axe 2 vers l'axe 1
On peut commencer par déplacer le sommet de la pile , le disque 4 vers l'axe 1, ce que l'on note 2 --> 1
Puis on peut faire 2 --> 3 , etc... Terminer
Regarder la suite des déplacements comme le parcours dans un arbre en profondeur, ce qui va nous aider à programmer la solution à ce problème de manière récursive
Créer une fonction récursive hanoi( a, b, n) où a et b peuvent prendre les valeurs 1 ou 2 ou 3 et n est le nombre de disques
Il faudra peut être mettre au point une fonction qui à partir de a et b donne l'axe auxiliaire c par exemple (1,2) --> 3 et (2,3) --> 1
Courbe de von Koch
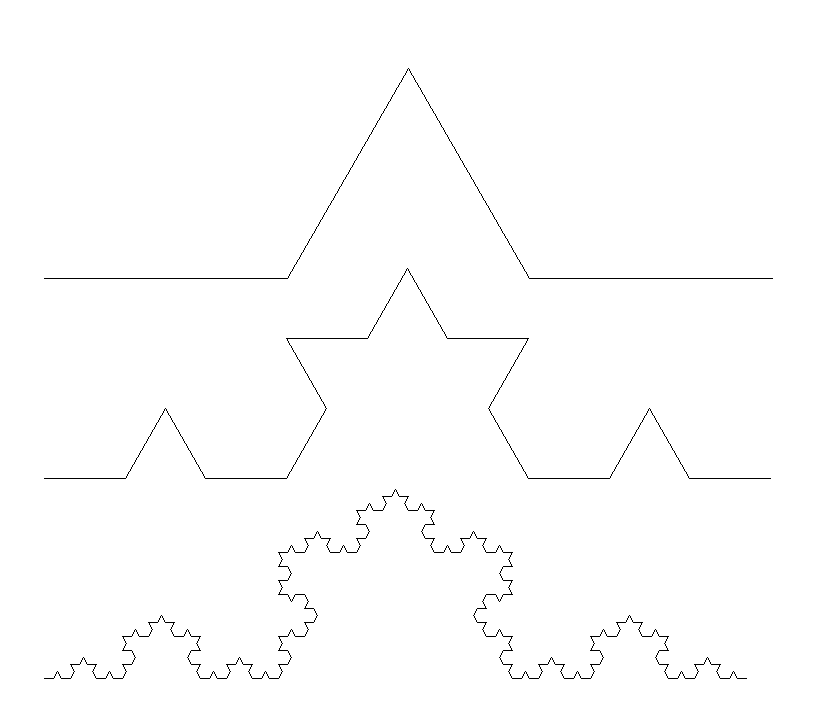
Nous allons dessiner dans un premier temps avec l'aide de la tortue (module turtle de python) la courbe de von Koch de manière récursive
Il s'agit de mettre au point la fonction koch(x,y,long,direction), où x et y sont les coordonnées de la tortue long la longueur du segment d'appui de la courbe et direction la direction de la tortue en (x,y)
Nous aurons besoin des fonctions trigonométriques cosinus et sinus du module maths car :
Etant donné deux points A et B dans le plan
$x_B = x_A + AB\times \cos(\theta)$ et $y_B = y_A + AB\times \sin(\theta)$
Avec $\theta = (\overrightarrow{u},\overrightarrow{AB})$
la règle est la suivanteCas simple:
Si la distance entre A et B est inférieure à un certain seuil par exemple 5 pixels alors la tortue trace une ligne droite reliant A et B
Sinon on appelle récursivement koch() sur [AC] sur [CD] sur [DE] et [EB]
Où C et D sont sur les tiers du segment [AB] et CED est un triangle équilatéral
Voici quelques exemples
Voici une façon de faire:
from turtle import *
from math import *
#--------------------------------------------------------
def koch(x,y,long,direction):
if long < 4:
setheading(direction)
forward(long)
else:
koch(x,y,long/3,direction)
koch(x + long/3*cos(radians(direction)),
y + long/3*sin(radians(direction)),
long/3,direction + 60)
koch(x + long/3*cos(radians(direction)) + long/3*cos(radians(direction + 60)),
y + long/3*sin(radians(direction)) + long/3*sin(radians(direction + 60)),
long/3,direction - 60)
koch(x + 2*long/3*cos(radians(direction)),
y + 2*long/3*sin(radians(direction)),
long/3,direction)
#-------------------------------------------
def flocon(x,y,longueur):
koch(x,y,longueur,60)
koch(x +longueur*0.5,y+longueur*sqrt(3)/2,longueur,-60)
koch(x+longueur,y,longueur,180)
#-------------Programme principal----------------
clearscreen()
speed(0)
hideturtle()
flocon(0,0,200)
En appelant 3 fois la fonction koch() on peut dessiner un flocon de neige

Une variante de la courbe de von Koch
On garde la même idée , c'est à dire la tortue avance et trace un segment si la longueur est en dessous d'une valeur critique mais on change de règle par exemple celle-ci illustrée graphiquement ci-dessous

On obtient alors ce genre de courbe:
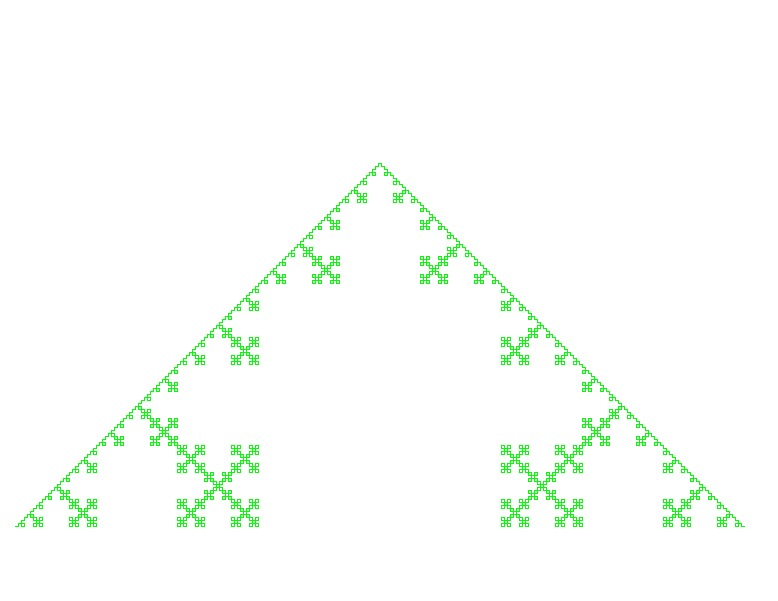
Variante: en dessous de la valeur critique la tortue trace une courbe polygonale
Si la longueur est en dessous d'une valeur critique la tortue n'avance pas de l et ne trace donc pas un segment de longueur l mais trace une ligne polygonale régulière dont la base a pour longueur l
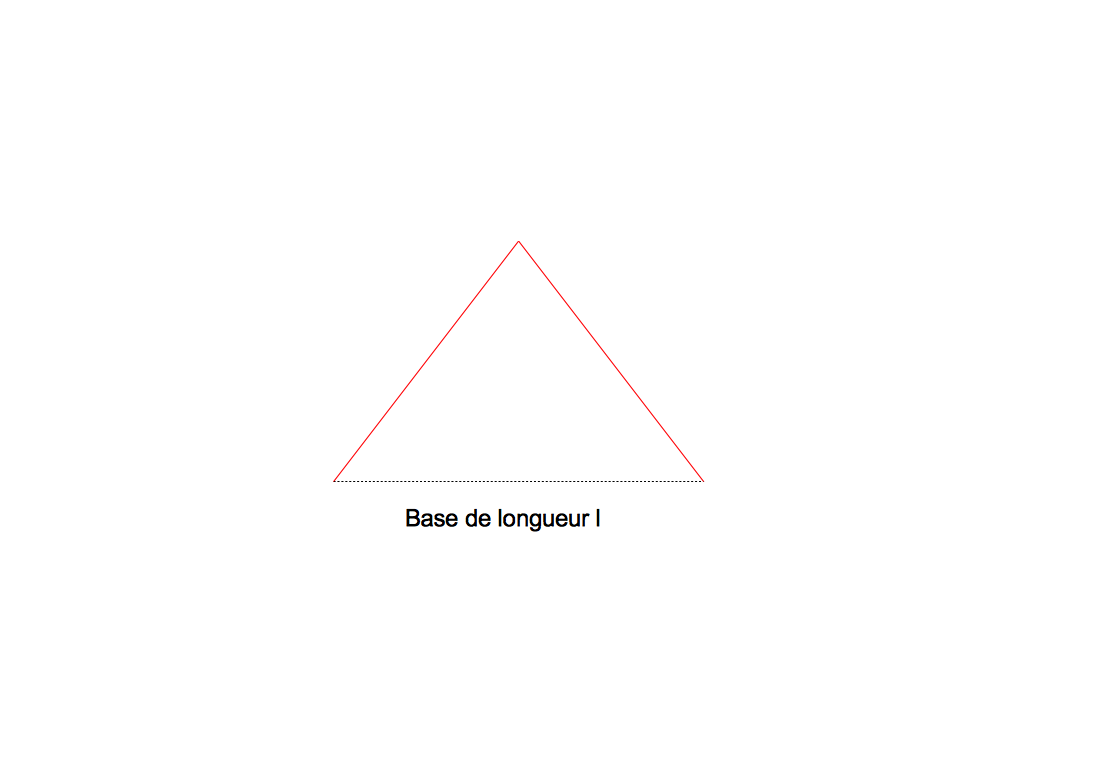
Il faut donc mettre au point au préalable une fonction qui fait tracer à la tortue une ligne polygonale comme un "accent circonflexe" la moitié du contour d'un carré.
Accent circonflexe
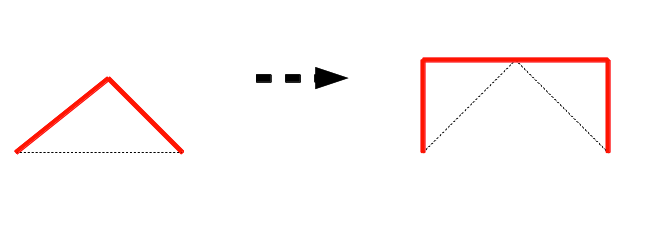
Puis définir une règle comme celle -ci:
On obtient alors la courbe du crabe:

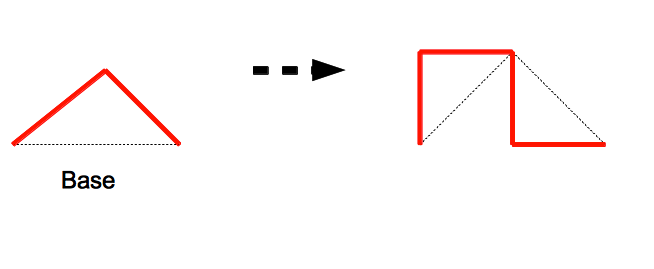
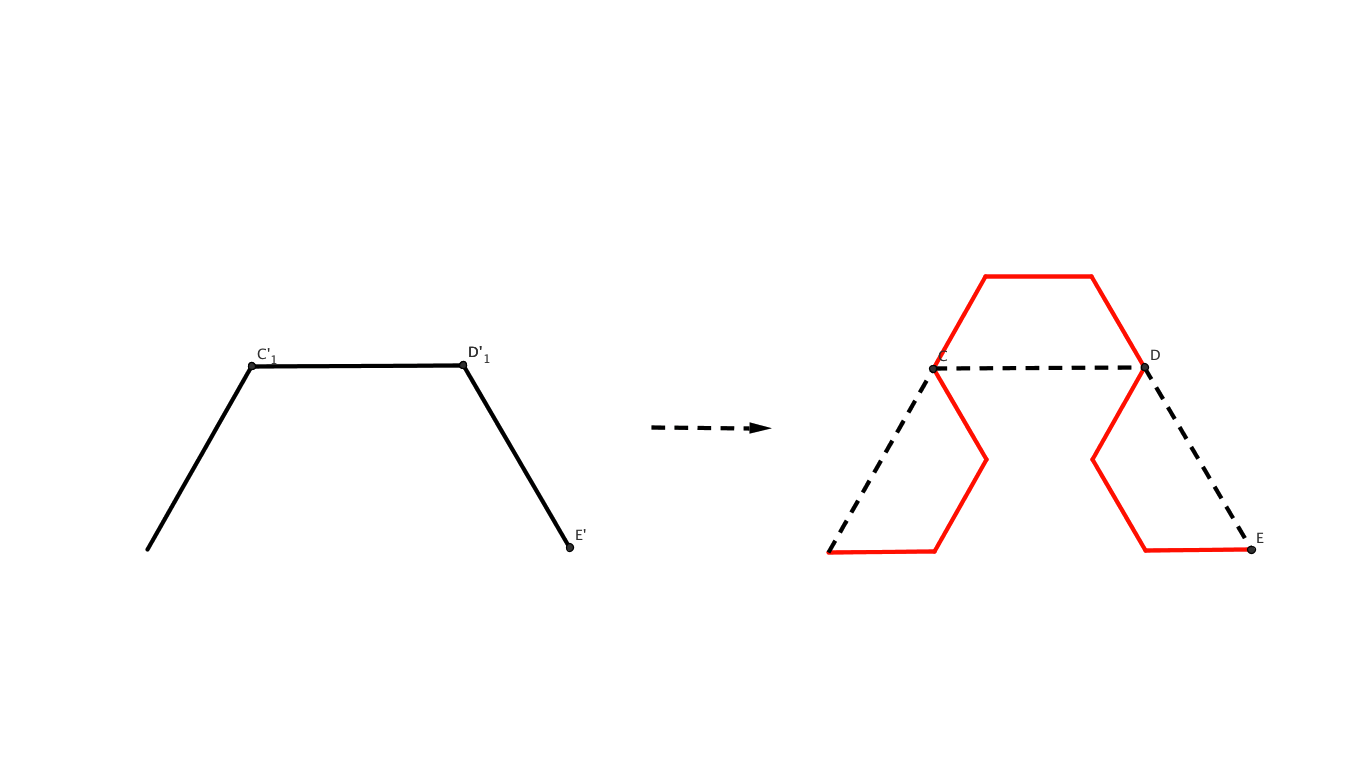
On définit souvent une règle de non-chevauchement :(voir ci-dessous) l'arc est une fois tracé d'un côté de la base, une fois de l'autre
On obtient alors la courbe du Dragon:

Trapèze
Cette fois-ci en dessous de la valeur critique la tortue trace une sorte de pont , contour de trois triangles équilatéraux imbriqués et de côté l/2:
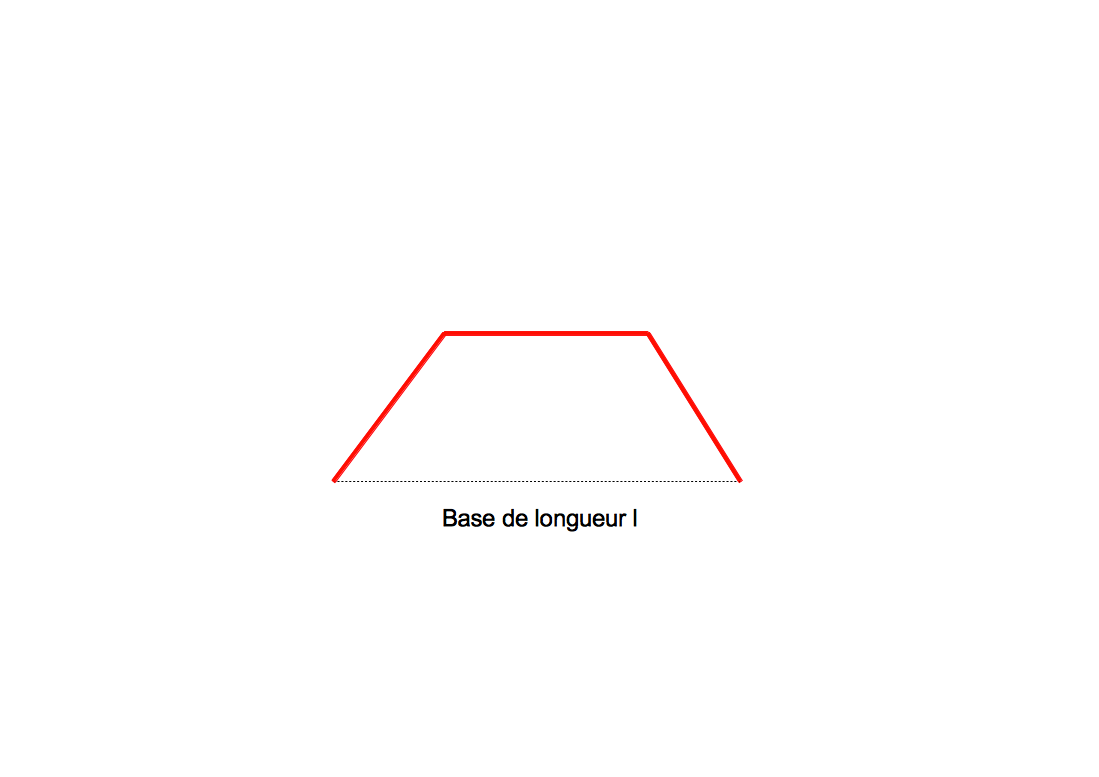
La courbe obtenue est le triangle de Sierpinski, si on utilise la règle ci-dessous

Autres Dessins
Faire une fonction récursive qui réalise un dessin similaire au dessin suivant
Puis du dessin suivant
Puis du dessin suivant
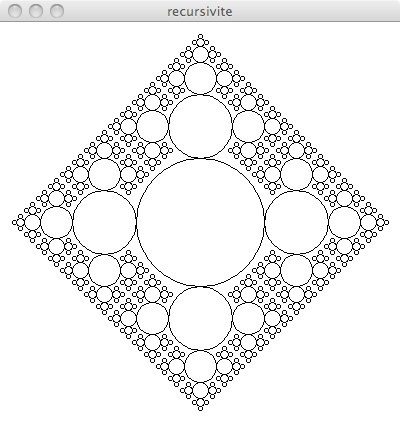
Un autre dessin
