Un exemple de projet

Attendus

1. Une introduction
2. Un cahier des charges
3. Quelques solutions informatiques aux problèmes posés
4. Le code commenté

Introduction

Il s'agit de programmer un classique des premier jeux vidéo : Asteroids

Un vaisseau spatial doté de trois vies doit faire exploser le plus possible d'astéroides

Une touche personnelle de créativité est la bienvenue par rapport au jeu initial

Le cahier des charges

Le cahier des charges est l'ensemble des contraintes fixées au départ. Au fur et à mesure que le projet avance celui ci est modifié

• Le jeu sera programmé avec le langage Java (plus précisément Processing)
• Un vaisseau spatial peut être déplacé avec les flèches directionnelles
• Si le vaisseau sort de la fenêtre graphique il revient dans la fenêtre à l'opposé
• Si on appuie sur la touche up il prend de la vitesse et lorsqu'on relâche la touche up il perd de la vitesse
• Avec les touches gauche et droite le vaisseau peut tourner sur lui-même
• Avec la barre espace il tire des missiles
• Des astéroïdes arrivent aléatoirement de tous les côtés
• Lorsqu'une missile touche un astéroïde celui-ci explose
• Si le vaisseau spatial est touché par un astéroide il perd une vie
• Le vaisseau spatial a trois vies
• Un bouton start permet de lancer le jeu (écran de départ)
• Sont affichés le score du joueur égal au nombre d'explosions d'astéroïdes et le nombre de vies restantes du joueur
• Quand le vaisseau n'a plus de vies le jeu s'arrête et l'écran de départ s'affiche

Analyse

Il y a trois éléments en interaction :

1. Le vaisseau
2. Les astéroïdes
3. les missiles

Puisque nous ne programmerons pas en utilisant la notion de classe, toutes les caractéristiques sont des variables globales, pour pouvoir être disponible en mémoire, de fonction en fonction

Caractéristiques du vaisseau

• Le vaisseau est une image au format png repérée par son centre par deux coordonnées x_vaisseau et y_vaisseau
• Le vaisseau est repéré aussi par un angle nommé direction
• Le vaisseau a une vitesse V (en norme)
• Le vaisseau a un nombre de vies nombreVies

Caractéristiques des astéroides

Caractéristiques des missiles

Quelques problèmes et leur solution

• mouvement rectiligne et uniforme d'un point

  on sait que distance parcourue = vitesse x durée , pour chaque coordonnée cela donne :

  $\Delta x =v_x\Delta t$

  $\Delta y =v_y\Delta t$

  Où $v_x$ et $v_y$ sont les vitesses constantes sur chaque axe

  Comment traduire cela d'un point de vue informatique ?

  Soit $x$ la variable représentant l'abscisse, et $\Delta t$ la durée de mise à jour de la fenêtre graphique par draw() de Processing ($\Delta t = \dfrac{1}{60}$ s ), la mise à jour de $x$ correspond à l'affectation $ x = x + v_x\Delta t$ (représentation paramétrique d'une droite)

  Cependant trop d'exactitude peut inutilement compliquer notre programme. L'information importante ici est que l'on ajoute toutes les $\Delta t = \dfrac{1}{60}$ s la même quantité constante la quantité $v_x\Delta t$ à $x$. Autant la renommer $v_x$ , l'initialiser $v_x = 1$ par exemple et écrire $x = x + v_x$

  
  //Variables globales
  int x,y,vx,vy;
  void initialisation(){
  x = ....;
  y = ....;
  vx = 1;
  vy = 2;
  .....
  }
  //-------------
  void miseAJourPosition(){
  x = x + vx;
  y = y + vy;
  }
  //------------
  void setup(){
  initialisation();
  }
  //------------
  void draw(){
  miseAjourPosition();
  }
  
  

• Mouvement uniformément accéléré

  

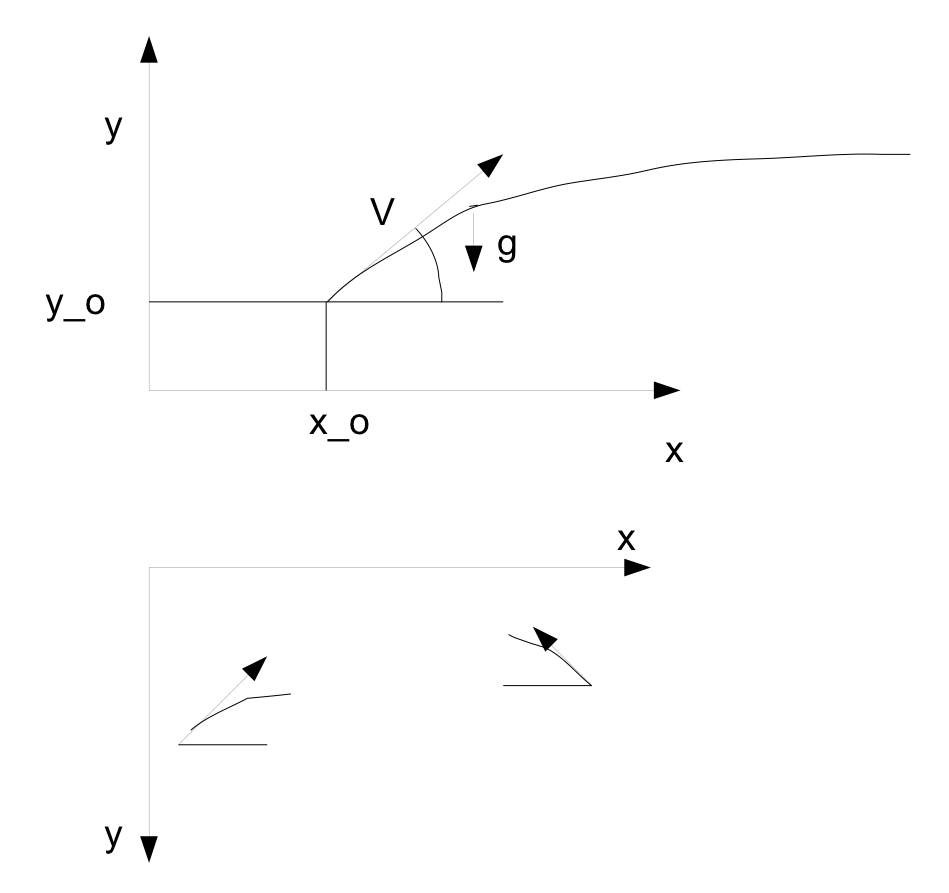
  On voit en physique en Terminale (graphique du dessus):

  $\left\{ \begin{aligned} x'' & = 0\\ y''& = -g \end{aligned} \right.$ primitivation $\left\{ \begin{aligned} x' & = V\cos (\alpha)\\ y'& = -gt+ V\sin (\alpha) \end{aligned} \right.$

  Finalement $\left\{ \begin{aligned} x & = V\cos (\alpha)t+x_0\\ y& = -g\dfrac{t^2}{2}+ V\sin (\alpha)t+y_0 \end{aligned} \right.$

  Comment l'adapter en informatique ?

  Il ne faut surtout pas le traduire tel quel mais dans le prolongement de ce qui a été fait précédemment mettre à jour d'abord la vitesse puis la position

  Enfin il faudra simplifier seul alpha sera une variable entrée via un slider (interactivité), V sera une constante

  Il faudra faire attention à la manière dont Processing gère les angles

  
  //Variables globales
  int x,y,vx,vy,V,g;
  //alpha sera entré via un slider (interactivité)
  float alpha;
  void initialisation(){
  x = ....;
  y = ....;
  g = 1; (à régler)
  vx = int(V*cos(alpha));
  vy = int(V*sin(alpha));
  .....
  }
  //-------------
  void miseAJourVitesse(){
  vy = vy + g
  }
  void miseAJourPosition(){
  x = x + vx;
  y = y + vy;
  }
  //------------
  void setup(){
  initialisation();
  }
  //------------
  void draw(){
  miseAJourVitesse();
  miseAjourPosition();
  }
  
  

• Comment faire tourner un objet sur lui-même?

  Processing n'a pas de fonction simple pour cela , la fonction rotate(float alpha) ne fait pas tourner une image sur elle-même d'un angle alpha

  Dans la partie Reference on peut lire :"Rotates a shape the amount specified by the angle parameter. Angles must be specified in radians (values from 0 to TWO_PI), or they can be converted from degrees to radians with the radians() function.

  Objects are always rotated around their relative position to the origin, and positive numbers rotate objects in a clockwise direction"

  De plus il y a un tutoriel à ce sujet où dans la partie "Rotating the correct way" on vous explique mieux l'intérêt de "Objects are always rotated around their relative position to the origin..."

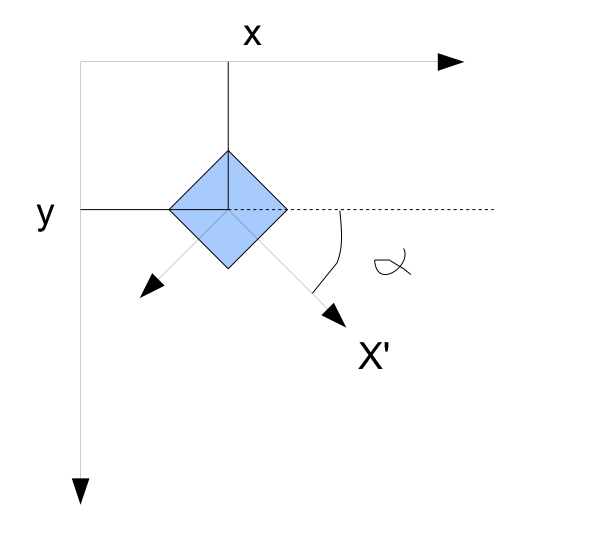
  L'idée est comme en mécanique, de suivre un objet dans "son repère", au centre de l'image. Or par défaut le repère est le coin supérieur gauche de la fenêtre graphique

  Durant tout le programme est mémorisé les coordonnées x et y du centre de l'image, pour emmener le repère par défaut (CSG) au centre de l'image on fait d'abord une translation de vecteur(x,y) d'où translate(x,y)

  On fait ensuite tourner le repère qui est au centre de l'image d'un angle alpha maintenant rotate(alpha)

  Puis on dessine l'objet en (0,0) du repère

  Par contre il faut remettre l'origine du repère au CSG pour les autres objets et remettre les axes comme ils étaient, pour cela la translation et la rotation sont mis dans une pile entre pushMatrix()et popMatrix()

  

  
  int x,y;//coordonnées du centre de l'image
  void tournerImage(float angle){
  pushMatrix();
  translate(x,y);
  rotate(radians(angle));
  imageMode(CENTER);
  image(nom_image,0,0,LARGEUR,HAUTEUR);
  popMatrix();
  }
  
  

• L'interactivité

  Comment est géré les clics de souris , les appuis sur les touches du clavier, les boutons les slidersetc...

• les explosions (sprites)

Ici il faut parler de la technique des sprites pour donner l'illusion des explosions

• Utilisation de classe Java externes

On utilisera comme une boîte à outils des classes Java déjà faites par exemple :

• pour l'interface graphique (GUI) pour l'utilisation de boutons (bouton start)
• On peut intégrer aussi du son avec la classe Minim de Processing, pour le tir des missiles et les explosions