Portes logiques

Implémentation et interface d'une porte logique

Une porte est une frontière entre un intérieur et extérieur

• l'extérieur est nommé interface de la porte logique (logic gate), ce qu'elle fait se traduit par une fonction logique (ou booléenne). Pour l'utilisateur (chip user) de la porte logique c'est le plus important
• L'intérieur est l'implémentation de la porte,comment elle fait à partir d'autres portes logiques (intégration) Pour le concepteur de la porte (chip builder) c'est le plus important
• Ce qui amène à un choix de porte(s) logique(s) primitive(s), celles dont l'implémentation sera matérielle et dépend de la technologie utilisée
• Nous admettons que toute fonction logique peut se décomposer en et, ou, non aussi on peut commencer avec les portes AND,OR ,NOT
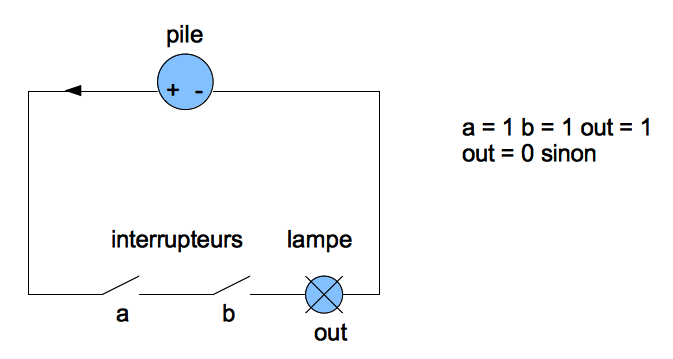
• Voici une implémentation de la porte AND avec deux interrupteurs en série

• Dans ce TP on considère la porte logique Nand (Non et) représentée par le schéma suivant comme primitive

• Voir ici une implémentation de la porte Nand avec des transistors

Logisim

Logisim est un logiciel de simulation écrit en Java,qui nous permettra de simuler et tester certaines portes logiques

Lancer Logisim à partir du répertoire isn

Portes logiques élémentaires

Il s'agit d'implémenter les portes Not,And,Or et Xor uniquement avec des portes Nand

Même si ces portes sont déjà à disposition dans logisim , nous allons utiliser la logique des sous-circuits (identique à celle des fonctions) pour créer un sous-circuit pour chacune de ces portes

1. Not

   Not(x) = Nand(x,x)

   Selectionner Add Circuit... dans le menu Project et entrer le nom du circuit Nand2Not

   Construire le circuit et tester le avec Poke

   

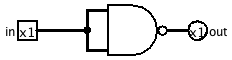
   Cliquer sur A pour pouvoir insérer du texte sur le circuit

   Ensuite cliquer sur le pin d'entrée et étiqueter in

   Faire de même avec le pin de sortie et étiqueter out

2. And

   And(x,y) = Not(Nand(x,y))

   Selectionner Add Circuit... dans le menu Project et entrer le nom du circuit Nand2And

   Par glisser-déposer prendre 2 pins d'entrée, un sous-circuit Nand2Not et une porte Nand

   Pour cabler Nand2Not on fait glisser la souris au-dessus de la porte pour faire apparaître les étiquettes d'entrée in et de sortie out

   Etiqueter les deux entrées in1 et in2 et la sortie out

   Construire le circuit

   

3. Or

   Sachant que Not(Or(x,y)) = And(Not(x),Not(y)), exprimer Or(x,y) uniquement à partir des portes Nand et Not

   Créer un nouveau sous-circuit Nand2Or

4. Xor(ou exclusif)

   Sachant que Xor(x,y) = Or(And(Not(x),y),And(x,Not(y))), créer un nouveau sous-circuit Nand2Xor

Portes logiques composites

• mux(x,y,sel) = Or(And(Not(sel),x),And(sel,y))

  la porte multiplexeur 2:1 permet de faire transiter sur un seul fil deux bits (l'un après l'autre) en fonction de la valeur d'un sélecteur sel

• Dmux(in,sel) = (x,y) si sel = 0 alors x = in et y = 0 sinon x = 0 et y = in

  Construire un circuit Dmux (démultiplexeur) à partir des portes Not et And

Arithmétique

1. Additionneur 1 bit

   Un additionneur 1 bit est vu comme deux fonctions booléennes s le chiffre des unités et cout la retenue de sortie dépendant de trois entrées

   3 entrées : deux bits a et b et une retenue d'entrée cin

   2 sorties : Le bit de résultat s et une retenue de sortie cout

   Après avoir fait la table de vérité des fonctions s et cout, on obtient comme circuit

   Créer un circuit add1 qui implémente l'additionneur 1 bit à partir du schéma ci-dessous

   

2. Additionneur 4 bits

   En utilisant 4 additionneurs 1 bit créer un additionneur 4 bits