TP : Fonctions
Factoriser le code
Il s'agit de simuler un des jeux du Chevalier de Méré, on lance 4 dés, si on a au moins un six on perd sinon on gagne
Dans un but de mise au point du programme on veut afficher le résultat des lancers
Dans une première approche ci-dessous, des lignes de code se répètent à plusieurs endroits du programme on va les mettre en ...facteur ou plutôt en ...fonction
Autre problème dans le but de faire des statistiques on aimerait répéter ce programme un grand nombre de fois
On va transformer finalement ce programme en une fonction qui retournera vraie si l'évènement "aucun six n'est sorti au cours des 4 lancers"
import random
#On simule le lancer de 4 dés
de1 = random.randint(1,6)
de2 = random.randint(1,6)
de3 = random.randint(1,6)
de4 = random.randint(1,6)
if de1 != 6 and de2 != 6 and de3 != 6 and de4 != 6:
print("Gagné ! ")
print("Le dé 1 vaut ",de1)
print("Le dé 2 vaut ",de2)
print("Le dé 3 vaut ",de3)
print("Le dé 4 vaut ",de4)
else:
print("Perdu ! ")
print("Le dé 1 vaut ",de1)
print("Le dé 2 vaut ",de2)
print("Le dé 3 vaut ",de3)
print("Le dé 4 vaut ",de4)
Une première factorisation est de lancer les 4 dés "en compréhension" et non pas "en extension", en mettant les lancers dans une liste construite en compréhension
On remplace les 4 lignes avec les variables de1,de2,de3 et de4 par:
lancers = [random.randint(1,6) for i in range(4)]
On généralise en créant une fonction appelée lancer_D(nb_lancers)
On dit que la variable nb_lancers est un argument de la fonction lancer_D
def lancer_D(nb_lancers):
return [random.randint(1,6) for i in range(nb_lancers)]
On peut encore factoriser
On va introduire deux fonctions
La première appelée afficher(lancers) affiche le résultat du lancer des dés contenu dans la liste lancers
La deuxième appelée aucunSix(lancers) retourne vrai si aucun six n'est dans la liste lancers
Finalement on obtient:
import random
#---------------------FONCTIONS---------------------------------------
def lancer_D(nb_lancers):
return [random.randint(1,6) for i in range(nb_lancers)]
#------------------------------------------------------------
def afficher(lancers):
for lancer in lancers:
print(lancer," ",end = " ")
#------------------------------------------------------------
def aucunSix(lancers):
resultat = True
for lancer in lancers:
resultat = resultat and (lancer != 6)
return resultat
#-----------------------------------------------------
def laBanqueGagne_unePartie(lancers):
if aucunSix(lancers):
return False
else:
return True
#------------------PROGRAMME PRINCIPAL------------------
lancers = lancer_D(4)
afficher(lancers)
print( laBanqueGagne_unePartie(lancers))
On constate que les fonction sont compréhensibles et nécessitent très peu de commentaires
Exercices
- Créer une fonction max(a, b) qui prend en paramètres deux entiers et retourne le plus grand des deux
- Créer une fonction min( a, b) qui prend en paramètres deux entiers et retourne le plus petit des deux
- Créer une fonction FToC( temp) qui convertit une température exprimée en degré Fahrenheit, en degré Celsius. On utilisera la formule T(°C) =T(°F)*1,8 + 32. Ray Bradbury a écrit un roman de science fiction intitulé Fahrenheit 451. Convertir 451 °F en °C
- Créer une fonction qui élève un entier au carré. Utiliser la dans une boucle pour calculer la somme des 100 premiers carrés
- Répéter un grand nombre de fois la fonction laBanqueGagne_unePartie(lancers) pour avoir une idée da la probabilité du joueur de gagner une partie
Un deuxième jeu du Chevalier de Méré consiste à lancer n fois deux dés.
Comme précédemment la Banque parie sur l'évènement A:"faire au moins un double six" et le Joueur parie sur l'évènement contraire
On a oublié pour combien de lancers n , p(A) > 0,5, faire une simulation pour retrouver cette valeur de n
Analyse
Déjà chez le philosophe français René Descartes on trouve une méthode d' analyse :

"...au lieu de ce grand nombre de préceptes dont la logique est composée, je crus que j'aurais assez des quatre suivants, pourvu que je pris une ferme et constante résolution de ne manquer pas une seule fois à les observer.
Le premier était de ne recevoir jamais aucune chose pour vraie que je ne la connusse évidemment être telle; c'est à dire d'éviter soigneusement la précipitation et la prévention; et de ne comprendre rien de plus en mes jugements que ce qui se présenterait si clairement et si distinctement à mon esprit que je n'eusse aucune occasion de le mettre en doute.
Le second, de : diviser chacune des difficultés que j'examinerais en autant de parcelles qu'il se pourrait et qu'il serait requis pour les mieux résoudre.
Le troisième, de conduire par ordre mes pensées, en commençant par les objets les plus simples et les plus aisés à connaître, pour monter peu à peu, comme par degrés, jusques à la connaissance des plus composés; et supposant même de l'ordre entre ceux qui ne se précédent point naturellement les uns les autres.
Et le dernier, de faire partout des dénombrements si entiers, et des revues si générales, que je fusse assuré de ne rien omettre." (Discours de la méthode).Par conséquent dès le début de la conception du programme il faut décomposer le problèmes en sous-problèmes suffisamment élémentaires
Programmation collective
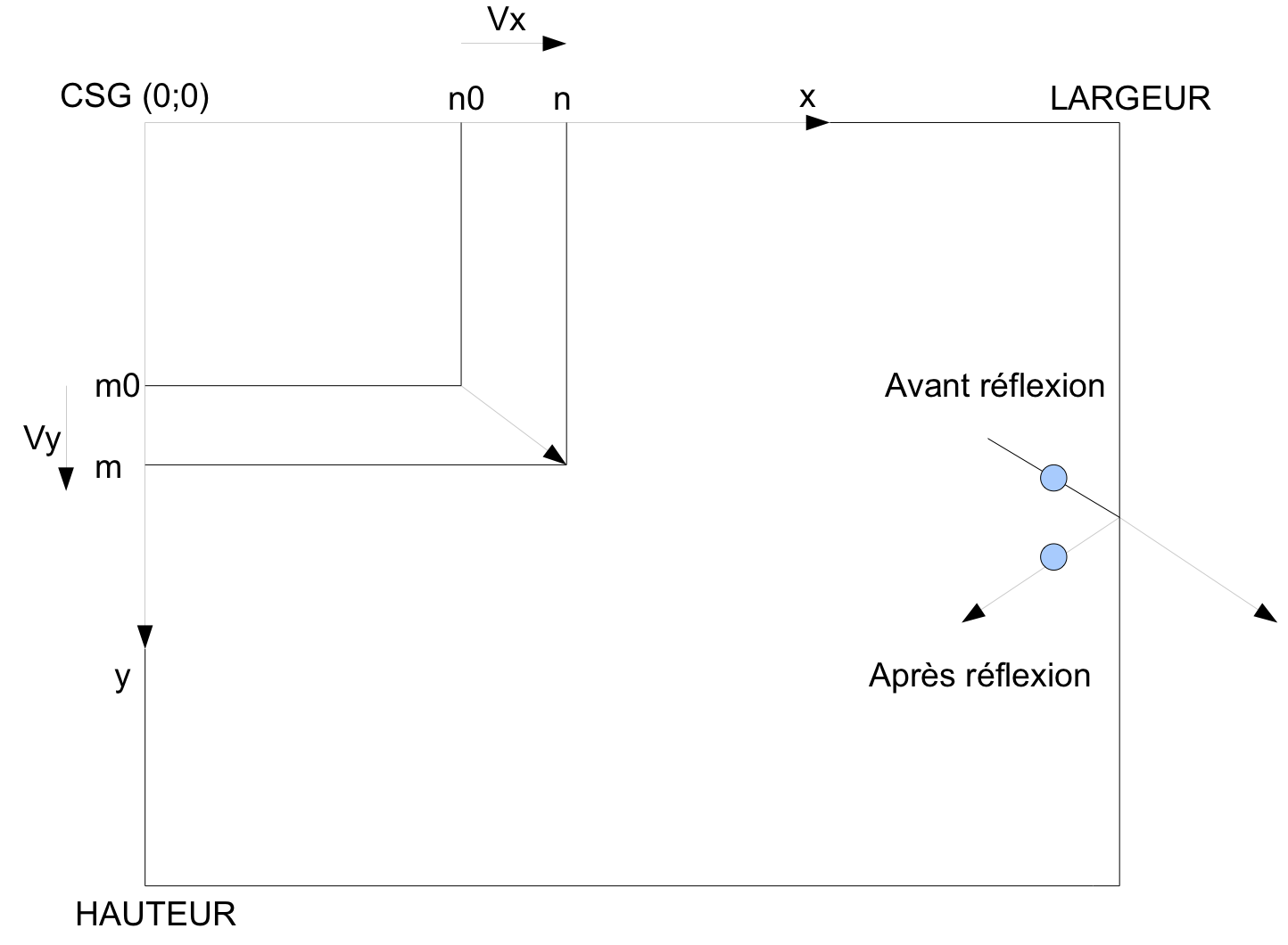
Il s'agit de faire un programme qui fait déplacer une balle rouge sur un fonds blanc. Cette balle rebondit sur les parois de la fenêtre
Le mouvement de la balle est une illusion : la balle est redessinée toutes les 10 millisecondes. Autrement dit si la position du centre de la balle est un couple d'entiers $(n_0;m_0)$ à un instant donné alors sa nouvelle position après 10 ms est $(n;m)$ tel que $n= n_0+v_x$ et $m=m_0+v_y$
La balle est repérée par ses coordonnées (x,y) et a un vecteur vitesse de coordonnées (vx,vy)
On déclare quatre variables globales de x,y,vx,vy et RAYON intialisé à 20
Télécharger le squelette du code ici et le compléter à partir des instructions ci-dessous
- Créer une fonction initialisationVitesse() qui initialise vx et vy aléatoirement avec des valeurs de l'ordre de l'unité positif ou négatif
Créer une fonction generationBalle() qui crée une balle blanche de rayon 20 pixels au centre du terrain et qui appelle initialisationVitesse()
Tester la fonction
-
Si vous testez le programme la balle va disparaître il faut à présent gérer les rebonds
Créer une fonction toucheBord() qui retourne vrai si la balle touche le bord de la fenêtre (tenir compte de la variable RAYON)
Créer une fonction reflexion() qui change vx et vy lorsque la balle touche le bord
Fonction et Python
En utilisant PythonTutor observer ce qui se passe pour le programme suivant
x = 1
def f(a):
a = a + 1
print(f(x))
print(x)
Que va afficher print(f()) dans le code suivant
var = 10
def f():
var = 20
def g():
return var
return g()
print( f())
Quel résultat pour ce code ?
x = 1
def f():
global x
x = 10
f()
print(x)