Recherche dans un tableau
Problématique
Etant donné un tableau et un élément définir une fonction estDansTableau(élément,Tableau) qui retourne vrai si élément est dans Tableau faux sinon
Il existe une fonction native en Python qui répond à ce problème, mais plus que la réalisation effective de cette fonction le but de ce TP est de découvrir aussi:
- La notion de test d'un programme avec le module python doctest
- La notion de complexité d'un programme pour pouvoir comparer l'efficacité des programmes réalisant la même tâche
- La notion de preuve de programme
La recherche en Table "simple"
La première idée est de parcourir le tableau du début à la fin et de tester à chaque fois si l'élément visité est celui qu'on cherche
Voici la fonction
estDansTableau(element,tableau)
parcourir le tableau
si on trouve element retourner Vrai
retourner Faux
La traduction en Python donne
def estDansTableau1(element,liste):
for x in liste:
if x == element:
return True
return False
Comment être sûr que la fonction répond effectivement au problème?
Est on sûr que cette fonction passera tous les tests possibles ?
Python a des modules qui permettent de tester une fonction. On présentera ici le module natif le plus simple, le module doctest
Nous avons déjà insisté sur l'intérêt de documenter une fonction éventuellement avant d'écrire la fonction dans le but justement de nous aider à écrire cette fonction
Voici sur l'exemple de la fonction précédente comment utiliser le module doctest
def estDansTableau1(element,liste):
'''Retourne Vrai si element est dans la liste liste,
Faux sinon
>>> estDansTableau1('b',[])
False
>>> estDansTableau1('a',['a'])
True
>>> estDansTableau1('b',['a'])
False
>>> estDansTableau1('b',['a','b'])
True
>>> estDansTableau1('b',['a','c'])
False
'''
for x in liste:
if x == element:
return True
return False
Dans la documentation on met quelques cas particuliers d'appel de la fonction qui nous paraissent les plus appropriés (a-t-on fait les bons choix ?) après le symbole de l'interpréteur et un espace et le retour attendu
Ensuite on ajoute l'instruction suivante pour pouvoir tester la fonction et on enregistre le fichier sous le nom recherche.py
if __name__ == "__main__": import doctest doctest.testmod()Ce qui donne en tout

Que signifient ces lignes de code ?
Un projet en Python n'est pas forcément écrit dans un seul fichier .py mais peut être découpé en plusieurs fichiers .py, pour améliorer la lisibilité du projet
Imaginons par exemple un projet dessinant des fractales à l'aide de nombres complexes
Il est préférable de mettre dans un fichier nbComplexe.py à part toutes les fonctions permettant de calculer avec les nombres complexes et de les tester avant de les utiliser dans un autre fichier pour dessiner des fractales
On peut les tester "à la sauvage" en appelant les fonctions sur des cas particuliers puis en faisant des print() un peu partout ou en utilisant doctest
Ensuite lorsqu'on appellera ces fonctions dans le module graphique fractale.py pour dessiner les fractales la partie test va bloquer ou au mieux ralentir l'exécution des dessins
Une façon de faire est de commenter tous les tests, une autre façon est de conditionner l'exécution des tests si le programme est lancé à partir de nbComplexe.py en écrivant pour cela if __name__ == "__main__":
Si le programme exécuté est fractale.py le programme principal est celui de fractale.py et non celui de nbComplexe.py dans ce cas les tests ne sont pas exécutés
Attention! on n'exécute pas le fichier recherche.py dans l'environnement intégré mais dans un terminal en faisant

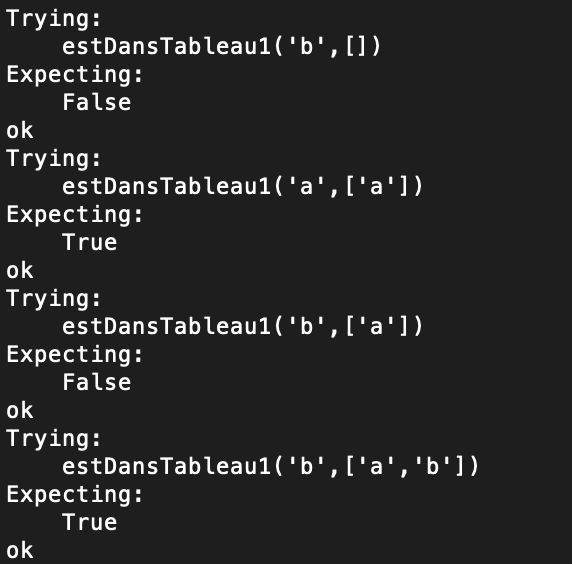
Voici ce que l'on observe dans le terminal si tout se passe bien
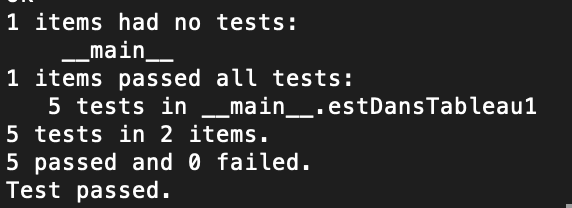
Quelques détails
Par contre si on oublie de parcourir tout le tableau en ne visitant pas le dernier élément du tableau, en changeant l'étendue du parcours de la liste

on observe alors que doctest signale un échec
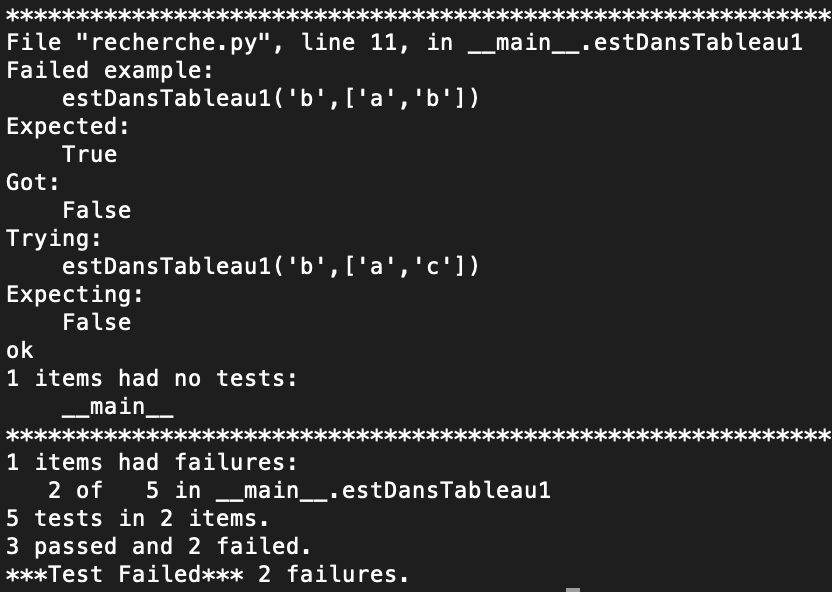
En conclusion si l'algorithme est simple et si des tests "pertinents" sont réussis on a l'impression légitime que la fonction réussira à tous les coups
Deuxième algorithme. Notion de preuve de programme
Cette fois-ci on parcourt le tableau avec une boucle Tant Que
On utilise pour cela une variable i initialisée à 0 et qui augmente de 1 pour chaque élément du tableau visité
def estDansTableau2(element,liste):
'''Retourne Vrai si element est dans la liste liste,
Faux sinon
>>> estDansTableau2('b',[])
False
>>> estDansTableau2('a',['a'])
True
>>> estDansTableau2('b',['a'])
False
>>> estDansTableau2('b',['a','b'])
True
>>> estDansTableau2('b',['a','c'])
False
'''
i = 0
while i < len(liste):
if element == liste[i]:
return True
i = i + 1
return i < len(liste)
On observe que la boucle est "moins simple" que la précédente et il nous faut être sûr qu'elle retournera le bon résultat quelque soit la liste et quelque soit l'élément
Cette fonction réussit les mêmes tests que la fonction précédente, mais a-t-on prévu tous les cas "difficiles"?
Nous allons voir une façon de prouver qu'une boucle réalise bien le travail escompté
D'une manière générale une boucle peut-être vue comme:
Tant Que E(v)
v <- f(v)
- v est une variable
- E(v) est une expression booléenne dépendant de v
- f une fonction
Dans le deuxième algorithme la variable est la variable i , l'expression booléenne est i < len(liste) et la fonction est la fonction i -> i + 1
Deux problèmes:
- Est ce que la boucle s'arrête à un moment c'est à dire existe-t-il une valeur $v_0$ de la variable v telle que $E(v_0)$ a pour valeur faux?
- Supposons que la liste a été parcourue jusqu'à liste[i-1], et que l'élément n'ait pas été trouvé, quelle action devons nous faire au rang suivant pour garder invariante cette propriété: (l'élément n'a pas été trouvé)? (Ce problème ressemble à une démonstration de l'hérédité dans un raisonnement par récurrence)
Prouver la fonction revient à résoudre ces deux problèmes
- La boucle finit par s'arrêter car la variable i augmente à chaque tour de boucle donc finira par être égale à len(liste)
- Augmenter i de 1 pourvu qu'on teste si liste[i] est égal à élément et dans le cas où ce test est négatif, il y a un tour de boucle supplémentaire et la propriété est encore vérifiée
l'algorithme de recherche simple dans un tableau est donc prouvé
Tests chronométrés
On va comparer la vitesse d'exécution des deux fonctions avec la fonction native de Python en faisant rechercher un élément dans un tableau de 500 000 éléments et où l'élément se trouve en dernière position dans la liste
On modifie le programme principal ainsi:
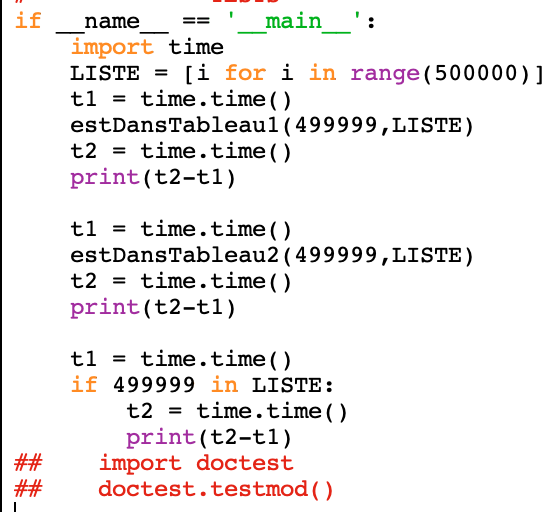
Voici ce que l'on obtient en secondes
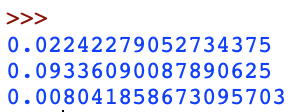
On observe que la fonction native in de Python est plus rapide que les deux fonctions estDansTableau(element,liste)
Nous allons voir à présent une façon plus rapide de rechercher un élément dans un tableau, la recherche dichotomique
Recherche dichotomique
Comment chercher un mot dans un dictionnaire ?
Parcourt on le dictionnaire du début à la fin ?
Surtout pas car le dictionnaire est ordonné et en utilisant le fait qu'il soit ordonné on peut procéder de manière plus efficace
On procède plutôt par dichotomie, (couper en deux) c'est à dire on ouvre le dictionnaire au milieu et on compare le mot du milieu au mot recherché
Si le mot recherché "est plus petit" que le mot du milieu on réitère la recherche dans la partie du dictionnaire qui précède le mot du milieu, sinon on réitère la recherche dans la partie qui suit le mot recherché
Quand s'arrête-t-on ? En général on s'arrête lorsqu'on a trouvé le mot cherché dans un petit nombre de mots contigus
Voici la fonction
estDansTableau3(element,tableau)
min <- 0
max <- longueur(tableau) - 1
milieu <- 0
Tant que min < max
milieu <- (min + max )//2
si tableau[milieu] = element
retourner Vrai
sinonsi element < tableau[milieu]
max <- milieu - 1
sinon
min <- milieu + 1
retourner element == tableau[max]
En Python cela donne:
def estDansTableau3(element,liste):
'''Retourne Vrai si element est dans la liste liste,
Faux sinon
>>> estDansTableau3('b',[])
False
>>> estDansTableau3('a',['a'])
True
>>> estDansTableau3('b',['a'])
False
>>> estDansTableau3('b',['a','b'])
True
>>> estDansTableau3('b',['a','c'])
False
'''
if len(liste) == 0:
return False
else:
min = 0
max = len(liste) - 1
while min < max :
milieu = (min + max )//2
if element == liste[milieu]:
return True
elif element < liste[milieu]:
max = milieu - 1
else:
min = milieu + 1
return liste[max] == element
Quelques remarques
- Cet algorithme ressemble à l'algorithme de dichotomie de résolution approchée de f(x) = 0, vu en cours de mathématiques
- Par contre les variables min et max ici doivent être des entiers car ce sont des indices d'un tableau, voilà pourquoi la division entière // et les deux instructions max = milieu - 1 et min = milieu + 1
Pourquoi ces deux instructions ?
Puisque on a déjà testé si element == tableau[milieu] autant restreindre la plage de valeurs d'une unité pour les recherches suivantes (voir la preuve plus loin)
Preuve
Terminaison:
L'écart entre min et max est divisé par 2 à peu près à chaque itération et donc finira par être nul et la boucle s'arrête
un invariant de boucle I(min,max) est pour tout k < min et k > max element != liste[k]
Initialisation
On peut considérer que element ne se trouve pas à l'extérieur du tableau
Hérédité
Si element n'est pas dans le tableau avant min et après max exclus et si element n'est pas l'élément médian alors si il est strictement plus petit que l'élément médian il n'est pas dans la partie de tableau plus grande que l'élément médian et si il est strictement plus grand que l'élément médian il n'est pas dans la partie de tableau plus petite que l'élément médian
Conclusion
A l'avant dernier tour de boucle min = max - 1 et par conséquent milieu = min donc si element < liste[milieu]=liste[min] alors max = min - 1 < min donc la boucle s'arrête et element n'est pas dans la liste
Si element > liste[milieu]=liste[min] alors min = milieu + 1 = min + 1 = max et la boucle s'arrête . Par contre il est possible que element soit égal à liste[max] d'où le test liste[max] == element
Test chronométrés
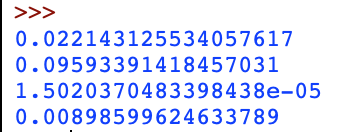
On observe que la recherche dichotomique est plus rapide que la recherche simple
Comment illustrer ceci autrement que par un test chronométré ?
Notion de complexité
Nous allons essayer de justifier la différence de temps d'exécution entre les fonctions de recherche en comptant le nombre de tests effectués pour une liste de n éléments
Pour les deux premières fonctions on teste les n éléments de la liste on dit alors que la complexité de ces fonctions est de l'ordre de n le nombre d'éléments de la liste
En procédant ainsi on s'affranchit des caractéristiques de la machine sur laquelle sera exécutée le programme et on donne une caractérisation universelle de l'algorithme en terme de complexité
Ce qui nous permet aussi de dire que si on multiplie la taille de la liste alors le temps d'exécution sera à peu près multiplié par 10
Combien de comparaisons pour la recherche dichotomique?
On observe que pour $n = 2^3=8$ on fera 3 comparaisons, pour $n = 2^4=16$ on fera 4 comparaisons, etc...
De manière générale on fera à peu près $\ln_2(n)$ comparaisons donc pour $n = 500\ 000$ on fera à peu près 19 comparaisons au lieu de $500 \ 000$!!!