TP 1: Exemples de suites récurrentes

Environnement de travail

Aller dans Outils >Lycée > Informatique >Python>IDLE ou utiliser wing 101

Faire new File pour ouvrir l'éditeur de texte pour pouvoir écrire un programme

A chaque fois qu'un programme est écrit le sauvegarder en faisant CTRL S. La première fois donner un nom significatif au programme, avec un suffixe .py

Ensuite pour exécuter le programme faire F5

Une suite arithmético-géométrique

On aimerait afficher le terme de rang $p$ de la suite $(u_n)$ définie par

$u_{n+1} = u_{n}\times \dfrac{1}{2} + 1$ avec $u_0 = 4$

$p$ étant un entier entré au clavier par l'utilisateur

On peut écrire $u_{n+1} = f(u_n)$ avec $f(x) = \dfrac{1}{2}x+1$

Dans un premier temps on va écrire une fonction Python qui calcule l'image d'un nombre $x$ par $f$

Puis on exécute cette fonction sur un cas particulier en faisant $f(4)$ et on affiche le résultat en faisant print(f(4))

Copier le code ci-dessous, le sauvegarder puis l'exécuter


def f(x):
#retourne l'image de x par la fonction affine f(x) = 0.5*x + 1
    return 0.5*x + 1

#-----------------Programme principal-------------------------------

#on fait exécuter la fonction pour calculer l'image de 4
#et on affiche le résultat à l'écran

print(f(4))

Pour afficher le terme de rang $p$ de la suite en partant de $u_0$ il suffit de faire une boucle et répéter $p$ fois l'affectation $u \leftarrow f(u)$

D'où la fonction terme(u0,f,p) ayant comme paramètres la valeur initiale $u_0$, la fonction $f$ et le rang $p$


def terme(u0,f,p):
#retourne le terme de rang p de la suite u_n = f(u_(n-1))
    u = u0
    
    for i in range(p):
        u = f(u)
    return u
        
#-----------------Programme principal-------------------------------

#on fait afficher  le terme de la suite de rang p
p = int(input(" Entrez le rang du terme de la suite ?  "))
u0 = int(input(" Pour quelle valeur initiale ?  "))
print(terme(u0,f,p))

Exercices

Donner différentes valeurs à $p$
Changer le valeur de $u_0$, par exemple prendre $u_0 = 1$
Changer la fonction affine, au lieu de 0,5 prendre -0,5 ou 1,5. Qu'observez vous ?
Que peut on conjecturer?
Changer la fonction, prendre par exemple $f(x) = 0,5\times(x+\dfrac{2}{x})$

Algorithme de seuil

Sans l'avoir prouvé on est "presque sûr" que le suite du début, décroissante et minorée par 2, "se rapproche" indéfiniment de 2, quelque soit la valeur initiale plus grande que 2

On aimerait avoir une idée de la "vitesse de convergence" de la suite

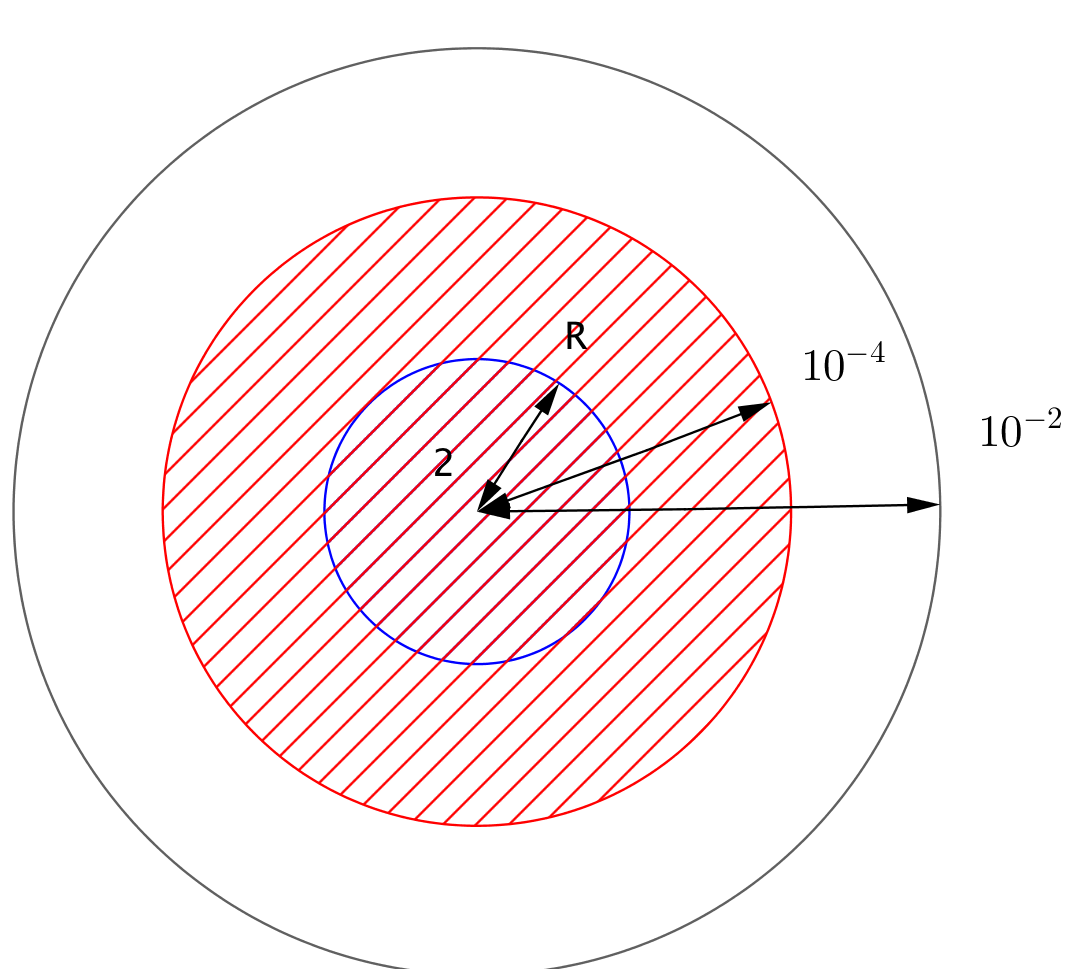
Une façon de faire est de fixer différents rayons $R$ autour de 2, par exemple 0,01 puis 0,0001 puis 0,000001 etc...et de regarder à partir de quel rang $n$ on a $u_n \leqslant 2+r$

Copier la fonction suivante et utiliser la



def rang(u0,f,seuil):

    u = u0
    indice = 0
    while u > seuil:
        u = f(u)
        indice = indice + 1
    return indice

Exercices

Pour $u_0 = 4$ que trouve t-on comme rangs pour les rayons $10^{-2}$, $10^{-4}$ et $10^{-6}$
Adapter la fonction rang() si on prend $u_0 < 2$ et répondre à la question ci-dessus
Modifier finalement la fonction rang() pour envisager à la fois le cas $u_0 < 2$ et $u_0 > 2$ (Indication: utiliser la fonction valeur absolue abs())
Conjecturer

Une suite croissante très rapidement

la suite de Sylvester est définie par

$s_{n+1} = (s_{n}-1)\times s_n + 1$ avec $s_0 = 3$

Exercices

Utiliser le squelette suivant sylvester.txt compléter le en suivant les questions suivantes, renommer le à votre nom, enregistrer le au format .py
Définir une fonction $g(x)$ en Python telle que $s_{n+1}=g(s_n)$
Utiliser cette fonction $g(x)$ et la fonction terme() pour afficher la valeur de $s_9$
Donner une fonction qui permet de calculer le nombre de chiffres de $s_9$ (faire une boucle de divisions par 10 tant qu'on peut)
Que peut on conjecturer?
Envoyer votre programme via l'ENT à votre professeur de maths avant Lundi 31/09/18