Sommes de Riemann
Calcul approché d'une intégrale avec Geogebra
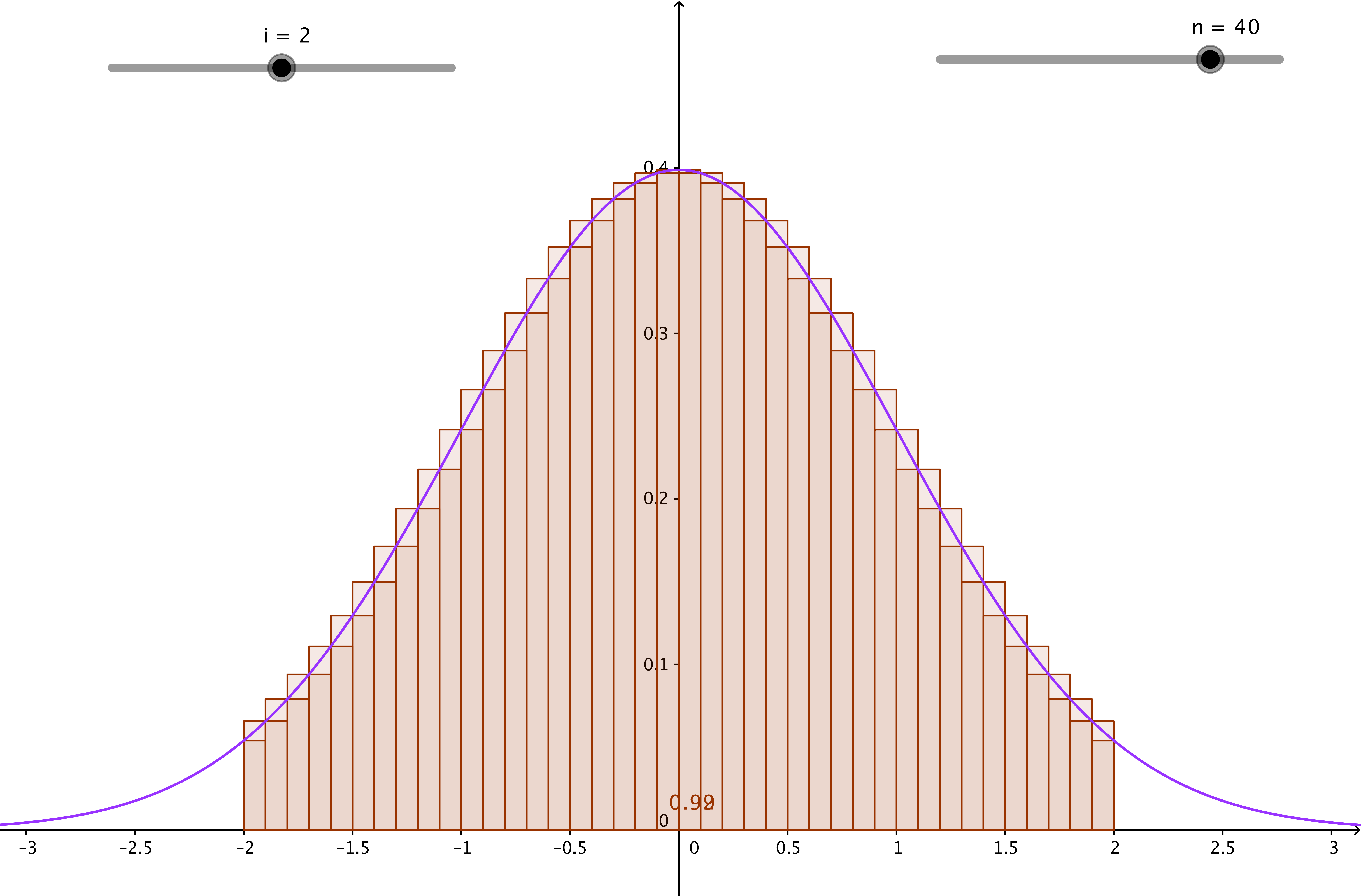
On veut calculer de manière approchée $\int\limits_{-i}^{i}\dfrac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}}\mathrm{d}x$ pour $i$ variant de 1 à 3
Définition: On appelle somme à gauche de Riemann de $f$ sur l'intervalle $[a;b]$ de pas $\dfrac{b-a}{n}$, la somme $\dfrac{b-a}{n}\sum\limits_{k=0}^{n-1} f(a+k\dfrac{b-a}{n})$
Théorème: Si $f$ est continue sur $[a;b]$ alors $\lim\limits_{n\to +\infty}\dfrac{b-a}{n}\sum\limits_{k=0}^{n-1} f(a+k\dfrac{b-a}{n}) \to \int \limits_{a}^bf(t)\mathrm{d}t$
Exercice
Ouvrir Geogebra et aller dans Options>Etiquetage>Pas les nouveaux objets
Entrer dans la barre de saisie $f(x)=\dfrac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}}$
Utiliser l'outil pour agrandir la courbe et la centrer à l'écran
- Créer un curseur $n$ qui sera un nombre entier variant de 1 à 50. Ce sera le nombre de rectangles
- Créer un curseur $i$ qui sera un nombre entier variant de 1 à 3. Ce sera la borne supérieure de l'intervalle d'intégration
Entrer dans la barre de saisie s = SommeInférieure[f,-i,i,n]
Qu'observez vous ? Faire varier $i$ et $n$
Entrer dans la barre de saisie s = SommeSupérieure[f,-i,i,n]
Qu'observez vous ? Faire varier $i$ et $n$
Entrer dans la barre de saisie s = SommeGauche[f,-i,i,n]
Qu'observez vous ? Faire varier $i$ et $n$
Entrer dans la barre de saisie s = Intégrale[f,-i,i,n]
Qu'observez vous ? Faire varier $i$ et $n$
Calcul intégral et tableur
On veut approcher $\int\limits_{-3}^{3}\dfrac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}}\mathrm{d}x$ par des sommes gauches de Riemann
Exercice
Ouvrir LibreOffice le tableur
Dans la cellule A1 entrer le nombre 20, ce sera le nombre de rectangles
Dans la cellule B1 entrer la formule = 6/A1, ce sera le pas de la subdivision
Dans la cellule C1 entrer le nombre -3, puis dans C2 entrer la formule = C1+B$1
Sélectionner la cellule C2 et la recopier vers le bas jusqu'à ce que vous obtenez comme nombre 3
Avez vous bien compris ce que fait la formule ci-dessus ?
- Dans la colonne D calculer les images des nombres de la colonne C par la fonction $f(x)=\dfrac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}}$
- Comment calculer la somme Gauche de Riemann de $f$ à partir des valeurs de la colonne D et le pas de la subdivision
- Augmenter le nombre de rectangles
- Qu'observez vous ?
Calcul intégral et Python
On veut approcher $\int\limits_{a}^{b}\dfrac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}}\mathrm{d}x$ par des sommes gauches de Riemann
L'utilisateur du programme peut entrer au clavier les bornes $a$ et $b$ et le nombre $n$ de rectangles
Exercice
- Faire un algorithme qui calcule la somme de Riemann à gauche de $f$ sur $[a;b]$ avec un pas de subdivision égal à $\dfrac{b-a}{n}$
- En déduire un programe Python
Est ce vrai que $\int\limits_{-2,58}^{2,58}\dfrac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}}\mathrm{d}x=0,95$ ?