Géométrie dans l'espace

Droites et plans dans l'espace avec Geogebra

Il s'agit en premier de visualiser les deux droites suivantes avec Geogebra

$d_1:\left \{ \begin{aligned} x &= 3 + a\\ y&=9+3a \\ z&=2 \end{aligned} \right.\qquad (a \in \mathbb{R}) \qquad d_2:\left \{ \begin{aligned} x &= 0,5 + 2b\\ y&=4+b \\ z&=4-b \end{aligned} \right.\qquad (b \in \mathbb{R})$

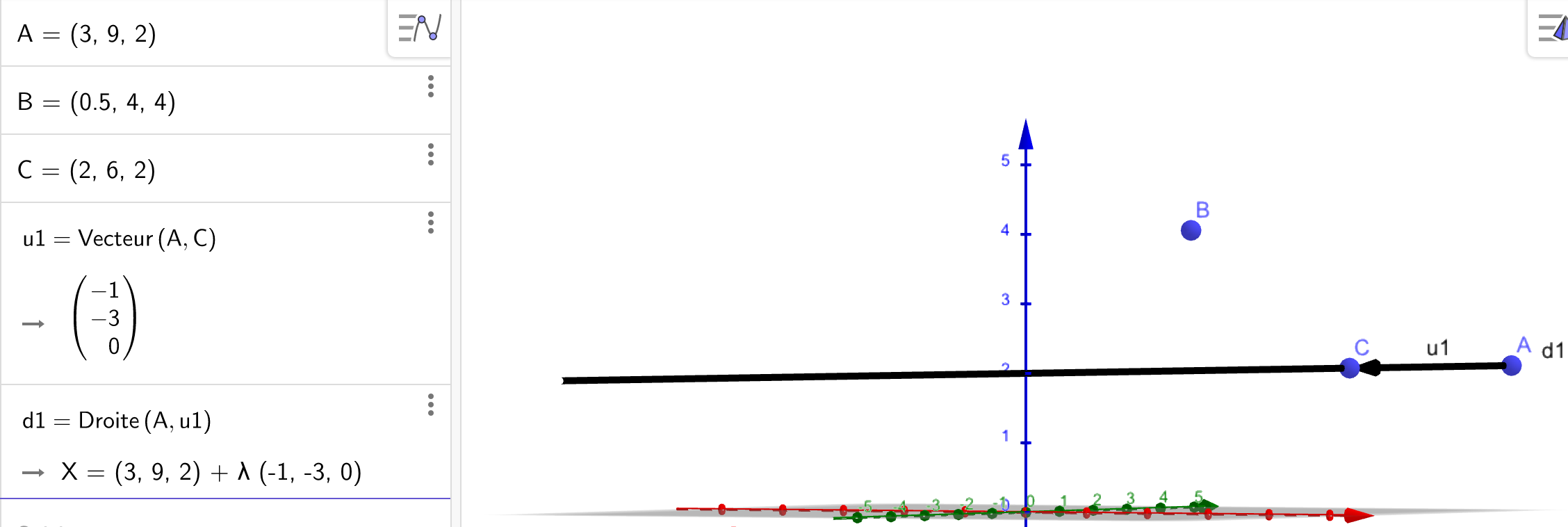
Dans un premier temps dans la barre de saisie on entre les coordonnées de deux points qui vont définir les deux droites

Par exemple on entre pour la droite $d_1$ le point A = (3,9,2) et le point C = (2,6,2) (on a pris a = -1)

Ensuite on peut visualiser un vecteur directeur u1 de $d_1$ en entrant u1 = Vecteur(A,C)

Ensuite on visualise d1 en entrant d1 = Droite(A,u1)

On observe dans la fenêtre Algèbre une représentation paramétrique de d1

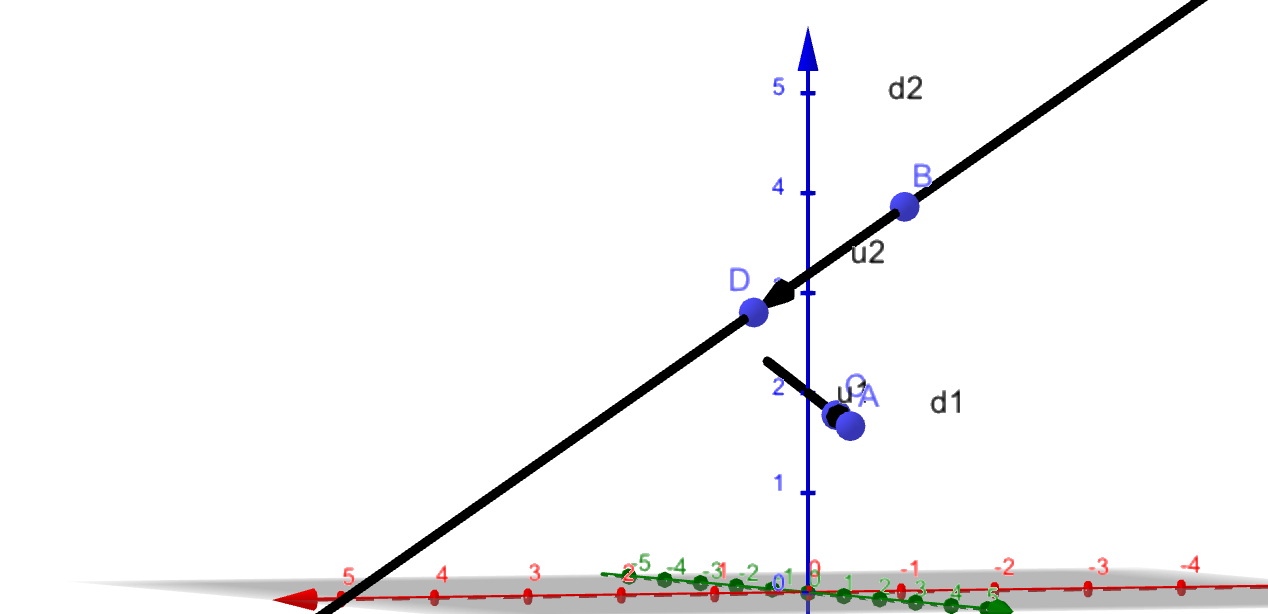
On fait de même pour la droite d2

On observe bien que les deux droites ne sont pas coplanaires

Ensuite on visualise le point S tel que S = (3,4,0.1)

Puis on définit le plan P1 par P1 = Plan(S,d1)

On observe que la droite d2 coupe le plan P1

Ensuite on définit le plan P2 par P2 = Plan(S,d2)

Les deux plans P1 et P2 se coupent selon une droite(en orange) que l'on visualise en cliquant sur l'outil "Intersection de deux surfaces"

On observe que cette droite qui passe par S, coupe à la fois d1 et d2

Droites et plans dans un tétraèdre

Afficher un tétraèdre

Construire une "médiane" reliant un des sommets S du tétraèdre au centre de gravité de la face opposée

Le sommet S appartient à 3 arêtes du tétraèdre et chacune de ses arêtes est associée à une arête opposée

A chaque fois qu'on enlève deux arêtes opposées les milieux des 4 autres arêtes définissent un plan

Visualiser les 3 plans et observer que la médiane issue de S coupe ces trois plans

Où ?