TP: Analyse de Fourier
Fonctions périodiques
Dans un premier temps nous allons construire avec Geogebra n'importe quelle fonction périodique de période T
Exercice
- Entrer dans la barre de saisie f(x)= x^2,0<= x < 2 Qu'observez vous ?
- Entrer dans la barre de saisie f(x)= (0<= x < 2)x^2 Qu'observez vous ?Quelle est la différence
Soit $f$ périodique de période $T$ nous supposerons que $f$ est construite à partir d'une fonction $g$ uniquement définie sur $[0;T]$ ainsi pour tout $x$ réel il existe $y \in [0;T]$ tel que $f(x)=g(y)$
Montrer que $y = x-E(\dfrac{x}{T})\times T$
En déduire un procédé pour tracer les fonctions périodiques suivantes
- $g(x) = x$ de période $2\pi$("signal en dent de scie")
Construire le signal carré de période $T=0.02$ s
telle que $f(t)= 10$ si $0 \leqslant t < 0.01$ et
$f(t) = 0$ si $0.01 \leqslant x < 0.02$ défini sur $[0;+\infty[$
Une façon de faire est d'abord de construire une fonction $g$ définie uniquement sur $[0;0.02[$ par :
g(x)= (0<=x<0.01)10 + (0.01<=x<0.02)0, 0 <= x< 0.02
Puis de définir la fonction f 0.02-périodique sur $R^+$ à partir de g ainsi :
f(x) = g(x-floor(x/0.02)0.02),x>=0
Analyse de Fourier
Fourier (1768-1830) est un mathématicien français qui a eu l'idée géniale d'analyser ("découper") toute fonction $2\pi$ périodique continue en somme de fonctions trigonométriques
Il est intéressant de donner un point de vue "géométrique" à cette analyse
Relativement à un repère orthonormé $(O,\ \overrightarrow{i},\ \overrightarrow{j},\ \overrightarrow{k})$ n'importe quel vecteur $\overrightarrow{u}$ peut se décomposer ainsi:
$\overrightarrow{u}=(\overrightarrow{u}.\overrightarrow{i})\overrightarrow{i}+(\overrightarrow{u}.\overrightarrow{j})\overrightarrow{j}+ (\overrightarrow{u}.\overrightarrow{k})\overrightarrow{k}$
Admettons que dans l'ensemble des fonctions $2\pi$ périodiques continues $f\otimes g = \frac{1}{\pi}\int\limits_0^{2\pi}f(t)g(t)\mathrm{d}t$ est un produit scalaire
Admettons que les fonctions $x \to \sin(nx)$ et $x \to \cos(nx)$ pour $n \in \mathbb{N}$ forment un repère orthonormé
Dans ce cas par analogie pour une fonction $2\pi$ périodique impaire $f$ définie par $f(x) = \dfrac{\pi - x}{2}$ si $x \in ]0,2\pi[$ et $f(n2\pi) = 0$ pour $n$ entier on obtient par analogie
$f \simeq \sum \limits_{k = 0}^{k = N} (f \otimes s_k)s_k$ où $s_k$ est la fonction définie par $s_k(x) = \sin(kx)$
Exercice
- Dessiner la fonction $2\pi$ périodique $f$
Il s'agit maintenant de prouver $f \otimes s_k=\frac{1}{\pi}\int\limits_0^{2\pi}\dfrac{\pi - t}{2}\sin(kt)\mathrm{d}t= \dfrac{1}{k}$
Soit $F(t)= -t\cos(kt)$. Calculer $F'$ en déduire que $\int -t\sin(kt)\mathrm{d}t = \dfrac{1}{n}(-F-\int \cos(nt)\mathrm{d}t)$
Finir le calcul
Avec Geogebra on va visualiser le fait que $f(x) \simeq \sum \limits_{k = 1}^N\dfrac{\sin(kx)}{k}$.
Cette approximation est d'autant meilleure que $N$ est "grand"
D'abord on va créer un curseur $n$ entier puis dans la barre de saisie entrer s(x) = Somme[Séquence[sin(kx)/k,k,0,n]]
Faire varier le curseur, qu'observez vous ?
Lorsque n = 5
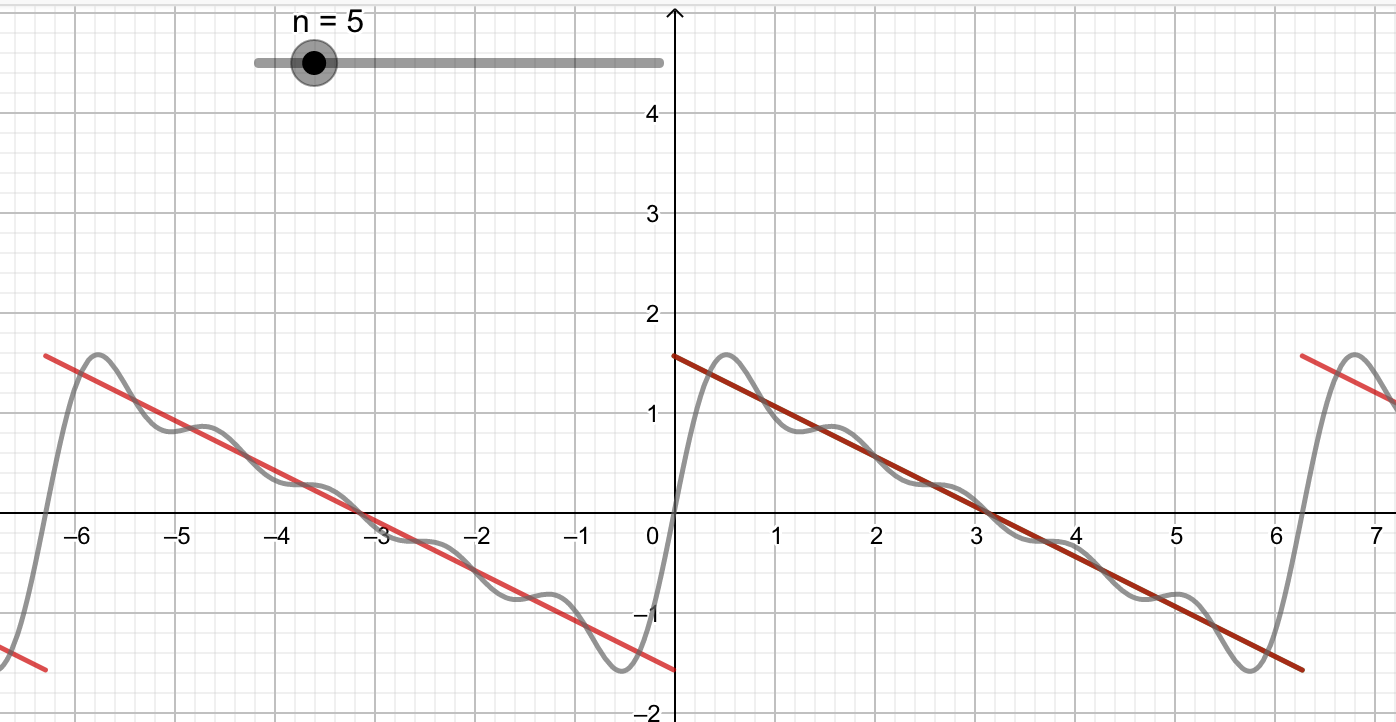
Lorsque n = 25
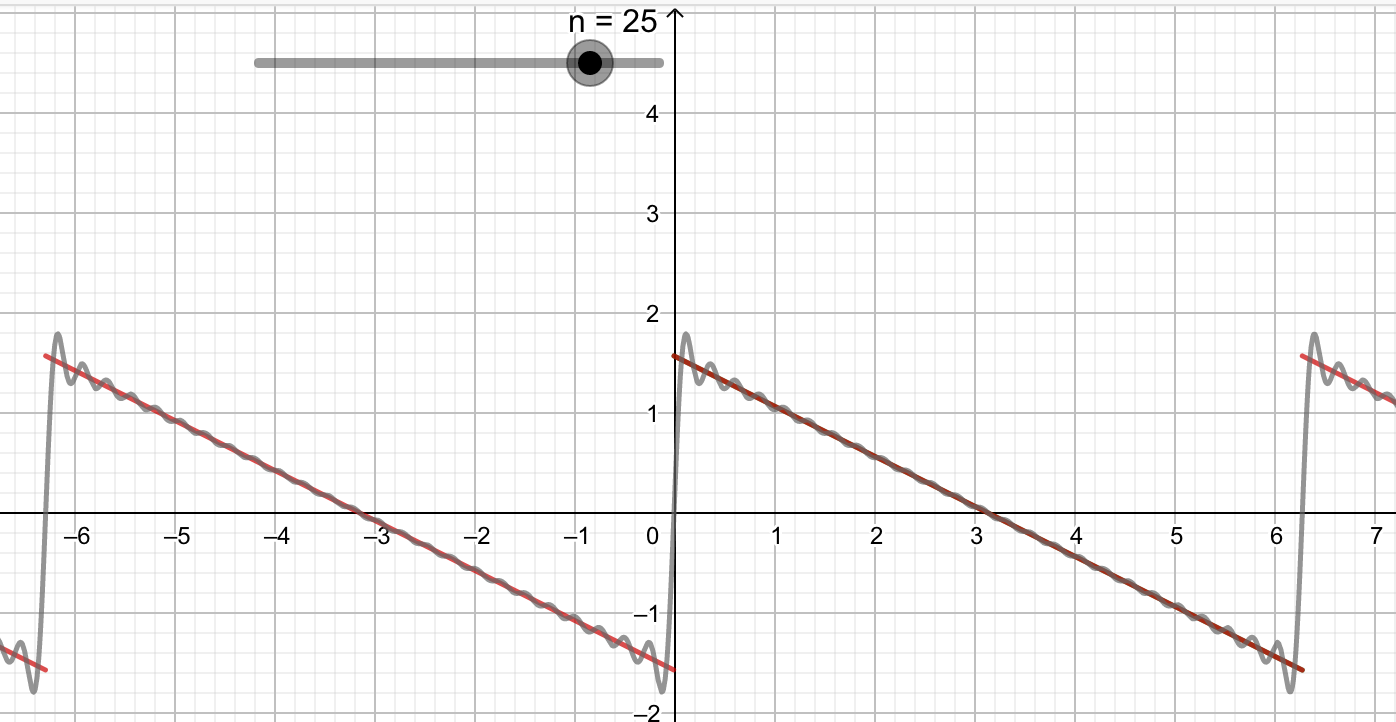
- Que se passe-t-il aux points de discontinuité ?