TP 3: Utilisation de Geogebra pour étudier des fonctions
Lieu orthoptique d'un cercle
Problème 1:
En assimilant une planète à une sphère , quelle orbite doit avoir un mobile autour d'une planète de telle sorte que de ce mobile "on voit" cette planète toujours à "angle droit"
Problème 2:
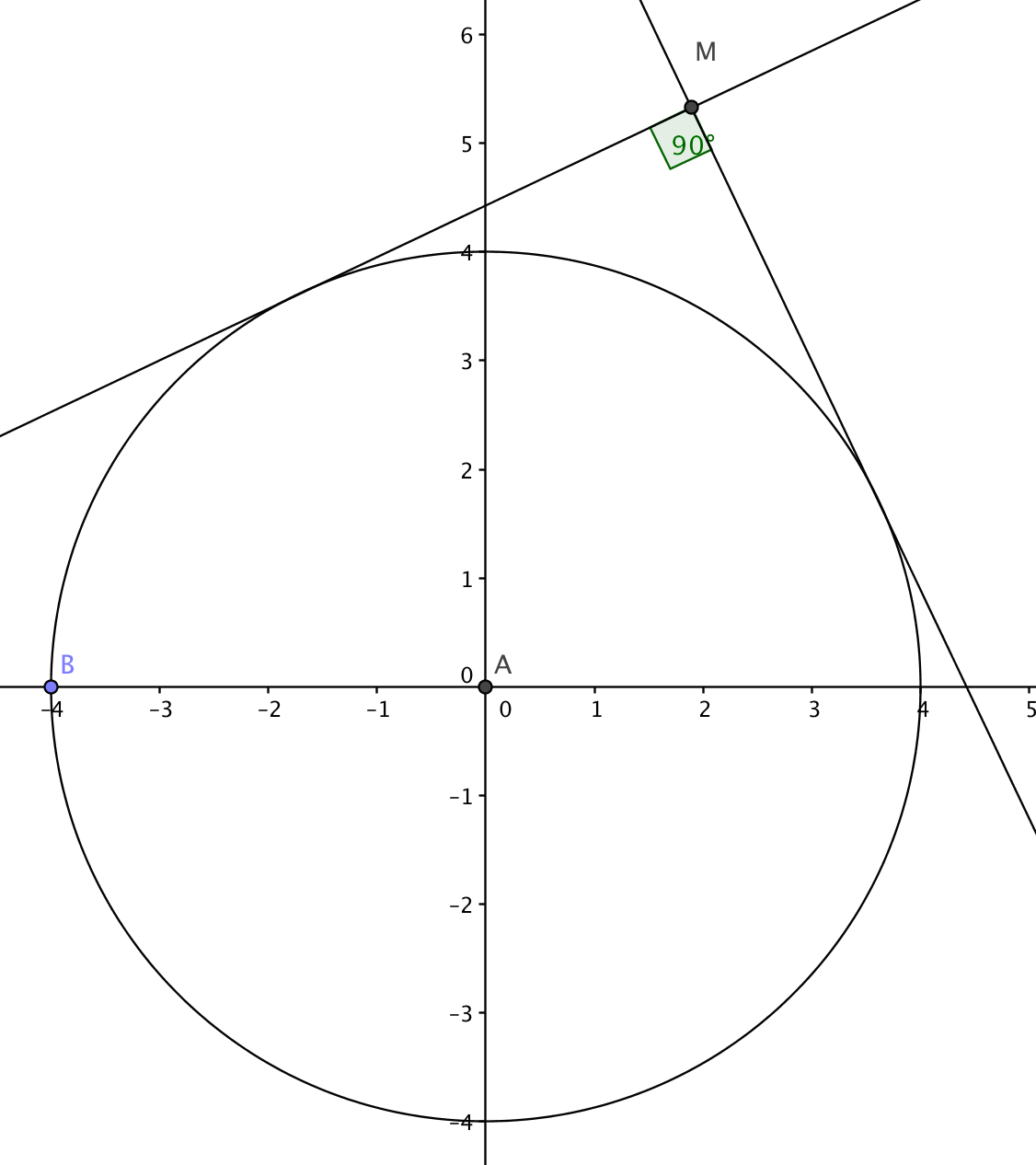
Etant donné un cercle C de rayon 4 , quel est l 'ensemble des points M du plan de telle sorte que les deux tangentes au cercle C issues de M sont perpendiculaires en M
Exercice 1
- Soit M un point cherché, A et B les deux points sur le cercle tel que les droites (MB) et (MA) sont perpendiculaires, que peut on dire des droites (OA) et (OB) ?
- Tracer avec Geogebra un cercle de centre l'origine et de rayon 4, puis sur ce cercle un point V variable
- Tracer en fonction de V un point M possible tel que (MV) soit une tangente au cercle et tel que l'autre tangente à C passant par V soit perpendiculaire à (MV)
- Activer la trace du point M (clic droit) et déplacer le point V. Qu'observez vous ?
Exercice 2
- Soit $f$ la fonction définie sur $[-4;4]$ par $f(x) = \sqrt{16-x^2}$. Entrer dans la barre de saisie , en bas de la fenêtre de Geogebra, la formule de la fonction $f$. Qu'observez vous ?
- Etudier la dérivabilité de $f$ (surtout en 4 et -4). Calculer la fonction dérivée
- Montrer qu'en tout point $A$ de coordonnées $(a;f(a))$ la tangente à la courbe de $f$ en $A$ est perpendiculaire à la droite (OA). (Utiliser le produit scalaire de deux vecteurs ou le résultat suivant: Dans un repère orthonormé deux droites sont perpendiculaires si et seulement si le produit de leurs pentes vaut -1)
- Calculer les coordonnées du point $M$
Reconstruction d'une courbe à partir de ses tangentes
Exercice
- Déterminer la formule d'un polynôme de degré 3 ayant pour racine -1, 1 et $a$ variant entre -5 et 5
- Construire un curseur $a$ variant entre -5 et 5
- Entrer dans la barre de saisie la fonction $f(x) = ....$ où les points de suspension sont à compléter par la formule trouvée ci-dessus
- Dans la barre de saisie entrer l'équation de la tangente à la courbe représentative de la fonction polynôme ci-dessus
- Activer la trace de la tangente et déplacer le curseur $a$, qu'observez vous ?
Etude de $f(x) = xE(\dfrac{1}{x})$ si $x \neq 0$ et $f(0)=1$
Exercice
- La fonction partie entière est notée floor() dans Geogebra. Tracer la courbe représentative de la fonction $x \rightarrow xE(\dfrac{1}{x})$. Que peut on conjecturer au sujet de la continuité de $f$ en 0 ?
- Prouver le
- Donner deux valeurs où $f$ n'est pas continue et le justifier par un calcul de limite
Fonctions périodiques et analyse de Fourier
Fourier (1768-1830) est un mathématicien français qui a eu l'idée géniale d'analyser toute fonction périodique continue sur $\mathbb{R}$ en somme de fonctions trigonométriques
Certaines fonctions périodiques, par exemple les signaux carrés ont des points de discontinuité
Que se passe-t-il en ces points ?
Dans un premier temps nous allons construire avec Geogebra n'importe quelle fonction périodique de période T
Exercice 1
- Entrer dans la barre de saisie f(x)= x^2,0<= x < 2 Qu'observez vous ?
- Entrer dans la barre de saisie f(x)= (0<= x < 2)x^2 Qu'observez vous ?Quelle est la différence
Soit $f$ périodique de période $T$ nous supposerons que $f$ est construite à partir d'une fonction $g$ uniquement définie sur $[0;T]$ ainsi pour tout $x$ réel il existe $y \in [0;T]$ tel que $f(x)=g(y)$
Montrer que $y = x-E(\dfrac{x}{T})\times T$
- En déduire un procédé pour tracer un signal en "dent de scie" Voir ici
- En déduire un procédé pour tracer un signal "carré"
Exercice 2
Construire le signal carré de période $T=0.02$ s
telle que $f(t)= 10$ si $0 \leqslant t < 0.01$ et
$f(t) = 0$ si $0.01 \leqslant x < 0.02$ défini sur $[0;+\infty[$
Une façon de faire est d'abord de construire une fonction $g$ définie uniquement sur $[0;0.02[$ par :
g(x)= (0<=x<0.01)10 + (0.01<=x<0.02)0, 0 <= x< 0.02
Puis de définir la fonction f 0.02-périodique sur $R^+$ à partir de g ainsi :
f(x) = g(x-floor(x/0.02)0.02),x>=0
- Un théorème d'analyse (Fourier) permet de montrer que pour tout $x$ en dehors des points de discontinuité on a $$f(x)= 5+ \sum\limits_{k=0}^{k=n}\dfrac{20}{(2k+1)\pi}\sin(100(2k+1)\pi x)$$ lorsque $n \to +\infty$
- Pour visualiser l'approximation ci-dessus créer d'abord un curseur $n$ entier
- Puis entrer s(x) = 5 + Somme[Séquence[20/((2k+1)pi)sin(100(2k+1)pi*x),k,0,n]],x >= 0
- Observer ce qui se passe aux points de discontinuité. Voir ici