Une tortue brownienne: Partie 2
Deuxième partie : Etude statistique
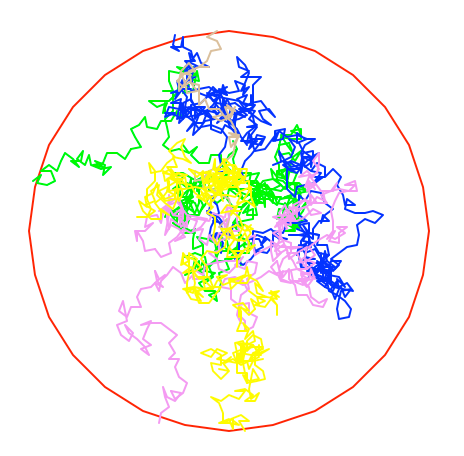
Nous allons maintenant faire des statistiques sur le déplacement de la tortue
Ci-dessus on peut voir 5 "marches aléatoires" de la tortue, pour chacune on peut calculer la longueur du chemin parcourue par la tortue, comme étant égale au produit du PAS par le nombre de tours de boucle "tant que"
On peut ensuite calculer la longueur moyenne et chercher une relation entre la longueur moyenne et le rayon du cercle limite SEUIL
Si on veut faire des moyennes sur au moins 1000 marches, il faut "désactiver" la partie graphique
Copier le programme ci-dessous, où est déjà donné une fonction distanceParcourueUneMarche() qui retourne la distance parcourue par la tortue au cours de cette marche, on vous demande d'écrire une fonction distanceMoyenneMilleMarches(pas,rayon) qui retourne la distance moyenne parcourue par la tortue au cours de ces 1000 marches
from math import *
from random import *
#----------------------------------------------------------
def estDansLeDisque(x,y,rayon):
'''retourne vrai si le point de coordonnées (x,y) est dans le
disque de centre (0,0) et de rayon rayon'''
return x*x + y*y < rayon*rayon
#----------------------------------------------------------
def distanceParcourueUneMarche(pas,rayon):
xT = 0
yT = 0
nbPas = 0
while estDansLeDisque(xT,yT,rayon):
i = randint(0,35)
angle = i*10
xT += pas*cos(radians(angle))
yT += pas*sin(radians(angle))
nbPas += 1
return nbPas*pas
#-------------------------------------------------------------
def distanceMoyenneMilleMarches(pas,rayon):
pass
#-------------------------------------------------------------
SEUIL = 100
PAS = 10
print("la distance moyenne parcourue pour 1000 marches est ",
distanceMoyenneMilleMarches(PAS,SEUIL))
Maintenant on cherche une relation mathématique expérimentale entre SEUIL le rayon du cercle limite et la distance moyenne parcourue par la tortue d_moy, sous la forme d'une fonction d_moy = f(SEUIL)
On va rechercher des fonctions f simples comme celles vues en cours d'année
Pour nous aider dans cette tâche on va tracer d_moy en fonction de SEUIL pour SEUIL variant de 20 à 100 , par pas de 20, en utilisant la bibliothèque python matplotlib
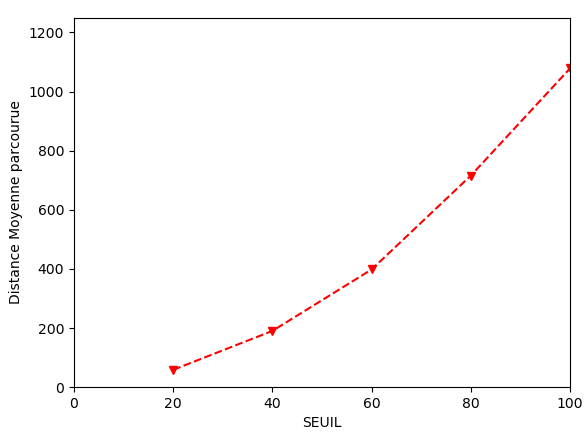
A la vue de la courbe ci-dessus quelle type de fonction peut on conjecturer entre d_moy et SEUIL ?
Mettre au point la relation conjecturée entre d_moy et SEUIL