TP 8: Récurrence et itération
Fonctions itératives et récurrence
Une fonction est itérative lorsqu'elle comporte une boucle for ou while
Dans ce cas la boucle va exécuter un certain nombre de fois une suite d'instructions, à partir d'un état initial, les entrées de la fonction, pour produire un état final voulu,le résultat de la fonction
Cela ressemble à une suite récurrente en mathématiques $x_n =f(x_{n-1})$ avec l'état initial $x_0$
Lorsqu'on veut prouver une propriété mathématique d'une suite récurrente, l'outil approprié est la démonstration par récurrence
Nous allons adapter ce type de démonstration pour avoir un outil qui
- nous aidera à construire la boucle (hérédité)
- justifiera que la boucle produit bien le résultat recherché
Exercices
- le drapeau français
Dans un tableau sont rangés dans le désordre les lettres B pour bleu, W pour white (blanc) R pour rouge
Il faut construire une fonction qui range le tableau en mettant en premier les lettres bleues B puis les blanches W puis les rouges R en parcourant le tableau une seule fois
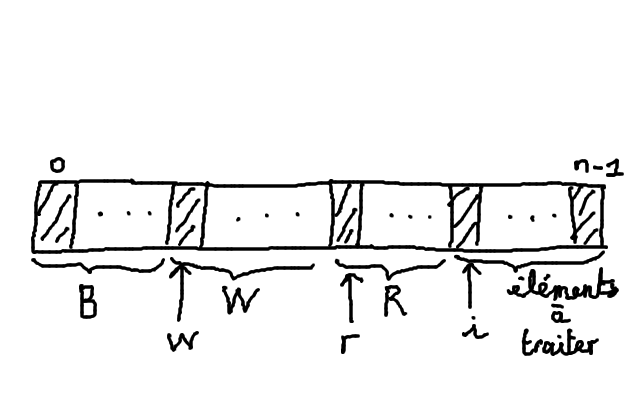
Nous allons formuler une hypothèse de récurrence:
Supposons que le travail soit fait jusqu'au rang i avec 0 <= i <=n-1 , ce qui signifie que nous avons réussi à classer les lettres B, puis les W puis les R au début du tableau en les repérant par des variables w et r entières où w est l'indice du début du bloc W et r le début du bloc R, 0 étant le début du bloc B
Montrons que en examinant le premier élément suivant d'indice i nous pouvons maintenir le rangement stable et faire le travail au rang i+1
Si l'élément d'indice i est blanc alors on échange les éléments d'indice i et r de place et on incrémente i et r
Si l'élément d'indice i est bleu alors on échange les éléments d'indice i et r de place puis les éléments d'indice w et r de place puis on incrémente i, r et w
Nous avons donc fait le travail au rang i+1
A l'état initial w = r = i = 0 et les trois blocs sont vides
Ce qui donne l'algorithme suivant
w = 0; r = 0; i = 0;
Parcourir le tableau T avec i variant de 0 à n-1 {
//n étant la longueur du tableau
Si T[i] est blanc alors{
échanger T[i] et T[r];
r++;
}
Sinon si T[i] est bleu{
échanger T[i] et T[r];
échanger T[r] et T[w];
r++;
w++;
}
i++;
}
On peut diminuer le nombre d'échanges dans cet algorithme en insérant le bloc à traiter entre les blancs et les rouges
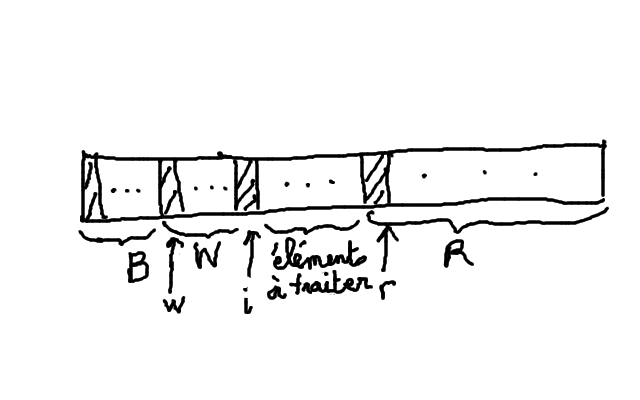
D'où l'algorithme :
w = 0; r = n; i = 0;
Tant que (i < r){
//n étant la longueur du tableau
Si T[i] est bleu alors{
échanger T[i] et T[w];
w++;
i++;
}
Sinon si T[i] est rouge{
échanger T[i] et T[r-1];
r--;
//ici i n'augmente pas d'une unité
}
Sinon{
i++;
}
}
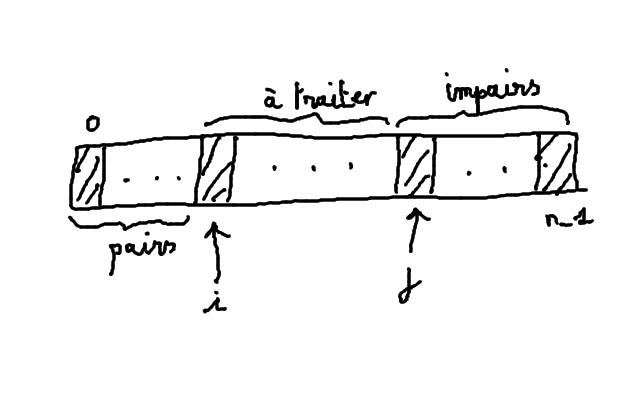
Il s'agit de trier un tableau contenant des entiers strictement positifs, de la manière suivante en tête du tableau on met les nombres pairs puis les nombres impairs
On va placer le bloc pair en tête du tableau puis les éléments à traiter puis les nombres impairs
D'où l'algorithme:
//n est la longueur du tableau
j = n; i = 0;
Tant que (i < j){
Si T[i] est impair alors{
échanger T[i] et T[j-1];
j--;
}
Sinon{
i++;
}
}
En processing cela donne:
void tri2(int[] tableau){
//on trie le tableau passé en paramètre
//les nombres pairs au début du tableau
//On maintient à chaque tour de boucle
//un bloc pair,en début de tableau,
//une zone à traiter puis un bloc impair
int i = 0;
int j = tableau.length;
while(i < j){
if(!estPair(tableau[i])){
echangeCellulesTableau(tableau,i,j-1);
j--;
}
else{
i++;
}
}
}
Une variante est de mettre le bloc à traiter en fin de tableau après le bloc pair et le bloc impair
D'où l'algorithme:
impair = 0;
Parcourir le tableau T de i = 0 jusqu'à n-1{
Si T[i] est pair{
échanger T[i] et T[impair];
impair++;
}
}
En Processing cela donne :
//On maintient à chaque tour de boucle
//un bloc pair,en début de tableau,
//un bloc impair puis la zone à traiter
void tri_2(int[] tableau){
int impair = 0;
for(int i = 0;i < tableau.length;i++){
if(estPair(tableau[i])){
echangeCellulesTableau(tableau,i, impair);
impair++;
}
}
}
