TP 7: Type composite : Tableaux

Type composite

"An array is a list of data. It is possible to have an array of any type of data. Each piece of data in an array is identified by an index number representing its position in the array. The first element in the array is [0], the second element is [1], and so on."(Reference)

Il y a deux types de variables : les variables de type primitif (int, float, double, boolean, char) et celles de type composite

Une variable de type Array est composée de plusieurs unités de même type primitif

Par exemple si on veut travailler avec les trinômes à coefficients entiers sous leur forme générale $ax^2+bx+c$ il est préférable d'avoir une seule variable désignant un trinôme que trois variables séparées pour a, b et c

Déclaration, Allocation et Affectation d'un tableau

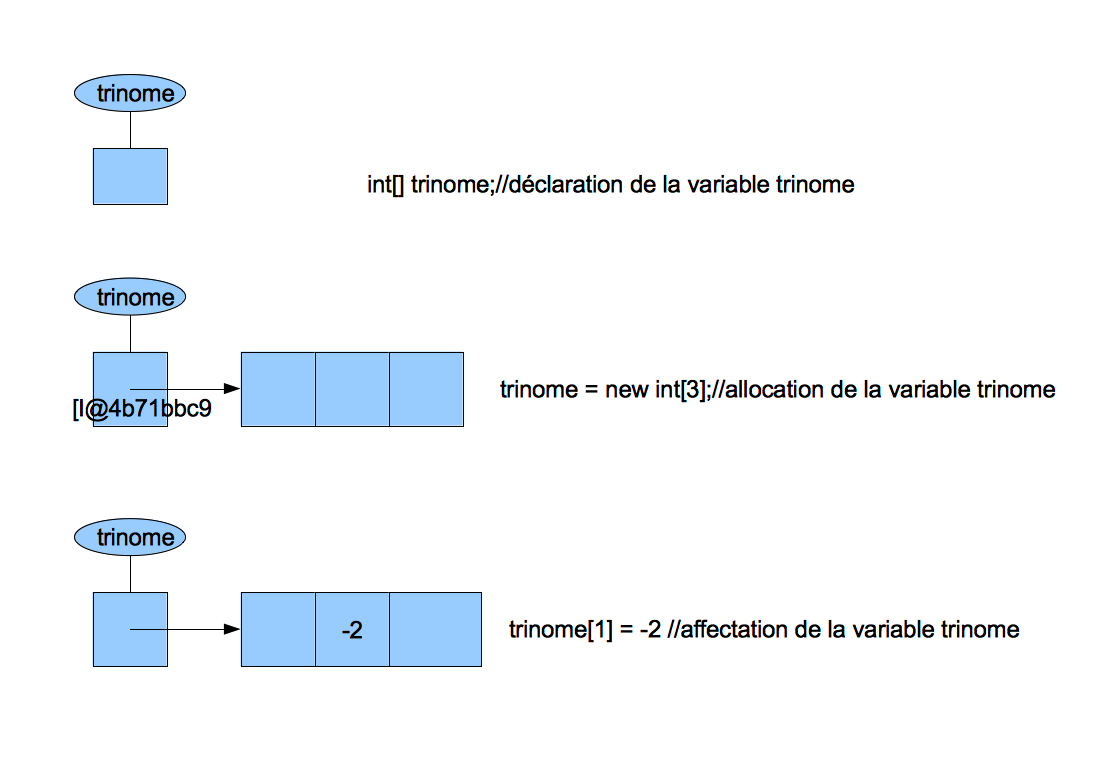
Pour préciser que l'on veut travailler avec un tableau d'entiers on déclare d'abord une variable de type tableau d'entiers ainsi

void setup(){
	//declaration de la variable trinome;
	int[] trinome 
}

A ce stade on a seulement un emplacement en mémoire (une adresse mémoire) il faut préciser de plus que l'on veut trois entiers ensemble

C'est la phase d'allocation de la variable trinome , on utilise la commande new qui construit un objet de type int[] composé de trois entiers

Par contre si on utilise println() à la place de print() dansla console est affichée :

[0] 0

[1] 0

[2] 0

Ce sont les contenus de trinome[0] , trinome[1] et trinome[2]. Ensuite si l'on veut travailler avec le trinôme par exemple $2x^2-x+3$ on va affecter la variable trinome ainsi

void setup(){
	//déclaration de la variable trinôme
	int[] trinome;
	//allocation de la variable trinome;
	trinome = new int[3] 
	//affectation de la variable trinôme
	trinome[0] = 3;
	trinome[1] = -1;
	trinome[2] = 2;
	
}

Exercices

1. Pour chacune des fonctions suivantes il faudra créer une fonction test

2. Créer une fonction afficheTrinome(float[] trinome) qui affiche en console le trinome sous forme mathématique

   Par exemple si trinome[0] vaut -1, trinome[1] vaut 2 et trinome[2] = 3 dans ce cas on affichera :

   3.0x^2 + 2.0x - 1.0

3. Créer une fonction trinome(float[] trinome, float x) qui calcule l'image de x par le trinôme en paramètre
4. Créer une fonction delta(float[] trinome) qui retourne un float et qui calcule le delta d'un trinôme
5. Créer une fonction sommeTrinome(float[] trinome1,float[] trinome2) qui retourne un tableau float[] somme des deux trinômes trinome1 et trinome2
6. Créer une fonction deriveTrinome(float[] trinome) qui retourne un tableau float[] la fonction dérivée du trinome
7. Créer une fonction coordonneesSommet(float[] trinome) qui retourne un tableau de deux variables de type float, les coordonnées du sommet de la parabole

La variable length de l'objet Tableau

"Each array has a variable length, which is an integer value for the total number of elements in the array. Note that since index numbering begins at zero (not 1), the last value in an array with a length of 5 should be referenced as array[4] (that is, the length minus 1), not array[5], which would trigger an error."(Reference)

De la même manière qu'une fenêtre graphique a des variables width et height qui la caractérisent, un tableau en tant qu'objet a une variable qui le caractérise c'est length

Par contre, il y a plusieurs tableaux qui peuvent être utilisés donc pour tel tableau nommé ceTableau si on veut connaître le nombre des éléments de ceTableau l'instruction ceTableau.length donne cette information

void setup(){
	int[] ceNombre = new int[100];
	println(ceNombre.length);
}

Exercices

1. Créer une fonction nbSuperieurADix(int[] tableau) qui retourne le nombre d'éléments supérieurs à 10 dans un tableau d'entiers

   On ne connaît pas à priori le nombre d'éléments du tableau d'entiers

2. Ecrire une fonction max(int[] tableau) qui trouve l'élément maximal dans un tableau d'entiers

Programmation collective

Le but est de calculer des termes de la suite de Sylvester u_n+1=u_n*(u_n-1)+1 avec u₀=2 au delà de ce qui est représentable en machine

On va utiliser un tableau grandNombre de longueur TAILLE initialisé à 200 dans lesquels seront stockés les chiffres de u_n

Il faut mettre au point les fonctions sommeGrandNombre(int[] grandNombre1,int[]grandNombre2) qui retourne un grandNombre, une fonction produitGrandNombre et afficheGrandNombre

Mini-projet personnel (avant J+7)

Est donné un tableau d'entiers tabEntier de taille quelconque. Il sera généré aléatoirement dans le setup() entre 10 et 30 inclus.

On l'affectera d' entiers positifs non nuls dans le setup()

1. Comme vous l'avez vu en TP vous rendrez les fonctions avec un jeu de tests et des fonctions test

2. (2 points) Créer une fonction afficheTableau(int[] tabEntier) qui affichera les éléments du tableau sur une même ligne séparé par un espace par exemple le tableau {2, 4, 5} sera affiché :

   2 4 5

   Prévoir un retour à la ligne après le dernier élément du tableau

3. (3 points) Créer une fonction tri1(int[] tabEntier) qui retourne un autre tableau de même taille dans lequel les éléments pairs sont à gauche (indices plus proches de 0) et les éléments impairs à droite

   Aide: On parcourt tabEntier avec une boucle for. Introduire deux variables indiceDernierPairRange initialisé à -1 et indiceDernierImpairRange initialisé à tabEntier.length

   Ces deux variables aident au rangement des nombres peu à peu. Supposez le travail effectué , c'est à dire dans le nouveau tableau des nombres pairs sont rangés de 0 à jusqu'au rang indiceDernierPairRange et des nombres impairs sont rangés de indiceDernierImpairRange jusqu'à tabEntier.length-1, lorsqu'on s'apprête à faire un nouveau tour de boucle et à examiner tabEntier[i]. Que faire si cet élément est pair ? et s'il est impair ?

4. (5 points) Créer une fonction tri2(int[] tabEntier) qui ne retourne rien mais fait le même tri que précédemment dans le tableau donné en paramètre tabEntier (on ne parcourt le tableau qu'une fois)

   Il faut le travail effectué précédemment, car la difficulté ici réside dans le fait qu'il faut faire le rangement dans le tableau donné