TP 3: Simuler le hasard

Environnement de travail

En plus de suivre ce texte en ligne , l'élève doit utiliser soit une version de Python locale au lycée ou en ligne par exemple ici

Un jeu du Chevalier de Méré

Ce jeu se joue avec deux joueurs, la banque B et un joueur A:

Une partie consiste à lancer 4 dés , si aucun six n'est sorti le joueur gagne

Voici un algorithme pour afficher le gagnant d'une partie . Au lieu de lancer 4 dés on lance 4 fois un dé et on s'arrête dès qu'un six est sorti

//On dispose d'une fonction lancerDe()
//qui simule le lancer d'un dé
nombre_de_lancers <- 0
D <- lancerDe()
Tant que D est different de 6 et nombre_de_lancers différent de 4
	D <- lancerDe()
	nombre_de_lancers <- nombre_de_lancers + 1
FinTantQue
Si nombre_de_lancers = 5
	aficher(le joueur A a gagné)
FinDeSi
Sinon
	afficher(la banque a gagné)
FinDeSinon

#importation du module random pour simuler le hasard
import random

#on lance une première fois un dé
D    = random.randint(1,6)
nombre_de_lancers = 1 
print "le lancer numero: ",nombre_de_lancers," est : ",D

#On relance au moins 3 fois à moins que le résultat soit 6
while D != 6 and nombre_de_lancers < 4:
	
    D = random.randint(1,6)
    nombre_de_lancers = nombre_de_lancers + 1
    print "le lancer numero: ",nombre_de_lancers," est : ",D
	
if D != 6:
    print "le joueur A gagne"

else:
    print "la banque gagne"

On veut à présent réaliser 1000 parties par exemple et calculer la fréquence de gain du joueur A

Pour factoriser le code on va traduire l'algorithme précédent en une fonction appelée le_joueurA_gagne() qui retourne deux valeurs VRAI ou FAUX

fonction le_joueurA_gagne()
	nombre_de_lancers <- 1
	D <- lancerDe()
	Tant que D est different de 6 et nombre_de_lancers < 4
		D <- lancerDe()
		nombre_de_lancers <- nombre_de_lancers + 1
	FinTantQue
	Si D différent 6 
		retourner VRAI
	FindeSi
	Sinon 
		retourner FAUX
	FinDeSinon

Cette fonction va être utilisée dans une boucle:

Compléter l'algorithme suivant pour qu'il affiche la fréquence de gain du joueur A pour 5000 parties

nb_parties_joueurA = 0
Pour nb_repetitions <- 1 jusqu'à 5000
	Si joueurA_gagne()
		nb_parties_joueurA <- nb_parties_joueurA + 1
#Calcul de la fréquence du gain du joueur A pour 5000 parties
........compléter ici..........

#importation du module random pour simuler le hasard
import random

#--------------------------fonctions------------------
def le_joueurA_gagne():
    D    = random.randint(1,6)
    nombre_de_lancers = 1 

#On relance au moins 3 fois à moins que le résultat soit 6
    while D != 6 and nombre_de_lancers < 4:
	
    	D = random.randint(1,6)
    	nombre_de_lancers = nombre_de_lancers + 1
   
    if D != 6:
    	return True

    else:
    	return False

#-------------------------------------------------------
#            Programme principal
#-------------------------------------------------------

nb_parties_joueurA = 0
for nb_repetitions in range(5000):
    if le_joueurA_gagne():
        nb_parties_joueurA  = nb_parties_joueurA + 1
#Affichage de la fréquence du gain du joueur A pour 5000 parties
print "la frequence de gain du joueur A est ",....compléter......

Conclusion

1. Qui a le plus de chance de gagner à ce jeu ?
2. Quel est la fréquence moyenne approximative de gain du joueur A ?

Une course aléatoire

Pour voir si vous avez bien compris l'étude précédente vous allez procéder de la même manière sur le problème suivant

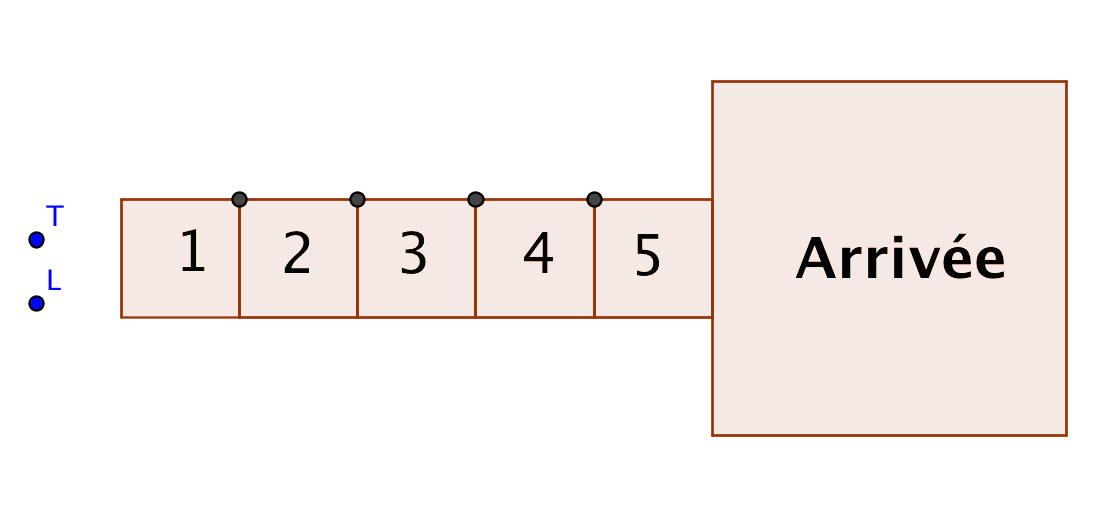
L (le lièvre) et T (la tortue) sont au départ d'une course. L'arrivée est six cases plus loin. Tant que l'un des deux joueurs n'est pas arrivé on lance un dé

Si le résultat est six le lièvre va immédiatement sur la case arrivée, sinon la tortue avance d'une case

Exercice

1. Faire quelques cas particuliers pour vous assurer d'avoir bien compris le problème
2. Faire un algorithme pour simuler une partie
3. Traduire cet algorithme en un programme et le tester
4. Faire un algorithme pour réaliser 1000 parties , puis faire un calcul de fréquences pour savoir lequel des deux joueurs a gagné le plus de parties
5. Traduire cet algorithmes en un programme et conclure