TP 14:Structure numérique d'une image
Structure numérique d'une image

Exercice
-
Télécharger chat.pgm une image au format pgm (binaire)
Télécharger chat_ascii.pgm une image au format pgm (ascii)
Télécharger chat.png une image au format png
- Aller dans Téléchargements puis faire clic-droit sur les icônes des fichiers images et noter leurs propriétés : Largeur, Hauteur et Poids en Ko
- Pourquoi est-il possible d'ouvrir chat_ascii.pgm avec l'éditeur de textes Gedit et non pas chat.pgm ?A quoi correspondent ces nombres que vous voyez ?
- Ouvrir chat.pgm avec l'application Jeex. Qu'observez vous ?
- Le début du fichier chat.pgm commence par 50 35 0A 23 ... Regarder avec Jeex dans la case ASCII que vaut 50 ? Que vaut 35 ?. Ne voyez vous pas une correspondance entre les deux débuts de fichiers chat.pgm et chat_ascii.pgm ?
Correction
- Vous avez normalement obtenu les informations suivantes
- Pour chat.png, taille = 48228 octets , largeur 320 pixels, hauteur = 240 pixels
- Pour chat.pgm, taille = 76861 octets même largeur et même hauteur
- Pour chat_ascii.pgm taille = 244 935 octets
- chat_ascii.pgm est un fichier codé en ASCII il peut donc être décodé par un éditeur de textes et on peut voir à l'écran des nombres, des lettres des symboles. chat.pgm est un fichier contenant des bits structurés en octets . Un éditeur de textes ne peut pas le lire
50 en hexadécimal noté 0x50 représente la lettre P en ASCCI ou le nombre 80 en décimal ou 01010000 en binaire.
35 représente en ASCII le nombre 5 en décimal 53 et en binaire 00110101
Or le début du fichier chat_ascii.pgm commence par :
P2
# CREATOR: GIMP PNM Filter Version 1.1
320 240
255
Donc ceci nous amène à penser que le début du fichier chat.pgm est similaire. P2 étant un code pour dire ascii et P5 binaire
-
1 octet est 8 bits. Un bit peut valoir 0 ou 1, la plus grande valeur que l'on puisse obtenir avec un octet est 1111 1111 qui vaut précisément 255 l'intensité maximale en nuances de gris (le blanc)
Donc pour chaque pixel de l'image chat.pgm, il y en a 320 x 240 = 76800 pixels, sa nuance de gris évoluant de 0 à 255 sera codée par un octet et ainsi sa taille sera approximativement 76800 octets
La différence de 61 octets correspond à l'en-tête du fichier
Pourquoi le fichier chat_ascii.pgm a-t-il pour taille 244 935 octets ? Si un pixel a une intensité de 1 il sera codé sur un octet 0x31 ,par contre si l'intensité est 128 alors cette intensité sera codé sur 3 octets 128 sera codé 0x31 0x32 0x38
Par contre chaque intensité est séparée par un caractère \n (passage à la ligne) codé sur un octet.
On peut estimer que les 76800 pixels ont besoin entre 3 ou 4 octets, d'où la taille comprise entre 230 400 et 307 200 pixels
- Le format png est un format compressé. On parlera de la compression dans un autre TP
Conversion en binaire et hexadécimal
Tout nombre entier $n$ strictement inférieur à 1 000 peut s' écrire sous la forme $n = a_0+a_1\times 10 + a2\times 10^2$ où $a_0$ est le chiffre des unités $a_1$ le chiffre des dizaines et $a_2$ le chiffre des centaines , ces chiffres sont compris entre 0 et 9
On écrit $n$ en base 10 ainsi $n = a_2a_1a_0$
Comment obtient on les chiffres ?
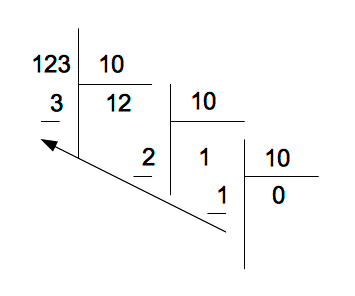
En divisant $n$ successivement par 10 jusqu'à obtenir un reste strictement inférieur à 10
Les restes successifs donnent les chiffres qu'il faut ensuite écrire dans le sens inverse
Regardons cela sur un exemple: $n = 123$
De la même manière tout nombre entier inférieur à 255 peut s'écrire $n = a_0+a_1\times 2+ a_2\times 2^2 +...+a_7\times 2^7$ où les $a_i$ valent 0 ou 1
$n=a_7a_6.....a_1a_0$ est la représentation de $n$ en binaire
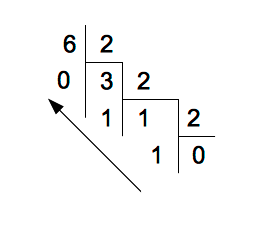
Par exemple $6=110$ et sur un octet $6=00000110$
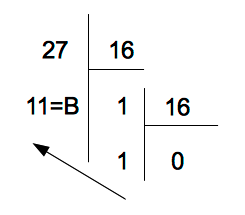
Pour la numération hexadécimale les 10 chiffres 0,1,2,3,4,5,6,7,8,9 ne suffisent plus puisqu'il faut 16 chiffres, car la base est 16. Par conséquent on rajoute les caractères A,B,C,D,E et F pour désigner ce qui habituellement l'est par 10,11,12,13,14,15
Pour convertir 27 en base 16 on divise 27 par 16 puis le quotient obtenu 1 par 16. En procédant comme précédemment on obtient 27 = 0x1B
L'intérêt de la base 16 est de rendre l'écriture des octets plus compact et plus lisible :
En effet tout octet $a_7a_6.....a_1a_0$ $=a_72^7+a_62^6+a_52^5+a_42^4+a_32^3+a_22^2+a_12+a_0$ $= 2^4(a_72^3+a_62^2+a_52+a_4)+(a_32^3+a_22^2+a_12+a_0)$
Les nombres entre parenthèses sont inférieur ou égaux à 15 donc on peut écrire un octet avec deux chiffres en base 16
Par exemple 255 = 1111 1111 en binaire et 255 = 0xFF
Ou encore 170 = 1010 1010 = 0xAA
Exercice
Télécharger binhex.pde le squelette de programme Processing avec lequel on va travailler
- Utiliser les différentes fonctions Test pour visualiser certaines conversions du décimal au binaire , du décimal à l'hexadécimal et réciproquement
- Construire une fonction itérative String decToBin(int n) qui fait le même travail que la fonction Processing binary()
- Construire une fonction récursive String decToBin(int n) qui fait le même travail que la fonction Processing binary()
