TP 12:La récursivité
Un exemple : la fonction Factorielle
La fonction factorielle est définie sur les entiers par $$n!=n\times (n-1)\times ... \times 1$$
le factorielle de n est le produit des n premiers entiers entre eux
Par exemple $4! = 4\times 3\times 2\times 1 = 24$
On peut programmer cette fonction de deux manières:
- itérative à l'aide d'une boucle for
- récursive
Recopiez le programme ci-dessous et testez le pour différentes valeurs 1,3,4, 5 et 17
int factorielleIteratif(int n){
int produit = 1;
for(int i = 1;i <= n;i++){
produit *= i;
}
return produit;
}
//----------------------------------
int factorielleRecursif(int n){
//Cas de base n = 1
if(n == 0){
return 1;
}
//n! = n * (n-1)!
else{
return n*factorielleRecursif(n-1);
}
}
//-------------setup----------------
void setup(){
println("le factorielle de 16 (itératif) est "+factorielleIteratif(16));
println("le factorielle de 16 (récursif) est "+factorielleRecursif(16));
}
La programmation d'une fonction récursive est basée sur deux idées
Pour un cas de base la fonction retourne une valeur
Pour la fonction factorielle pour n = 0 la fonction retourne 1
Pour la cas général n > 1 dans le corps de la fonction il y a un appel à la fonction elle même mais sur une valeur inférieure à n
On peut ainsi traduire $n!=n\times (n-1)!$
Exercices
- Construire deux fonctions, l'une itérative et l'autre récursive permettant d'ajouter les n premiers entiers entre eux
- Construire deux fonctions, l'une itérative et l'autre récursive permettant d'ajouter les inverses des n premiers entiers entre eux
Arbre des appels de fonctions
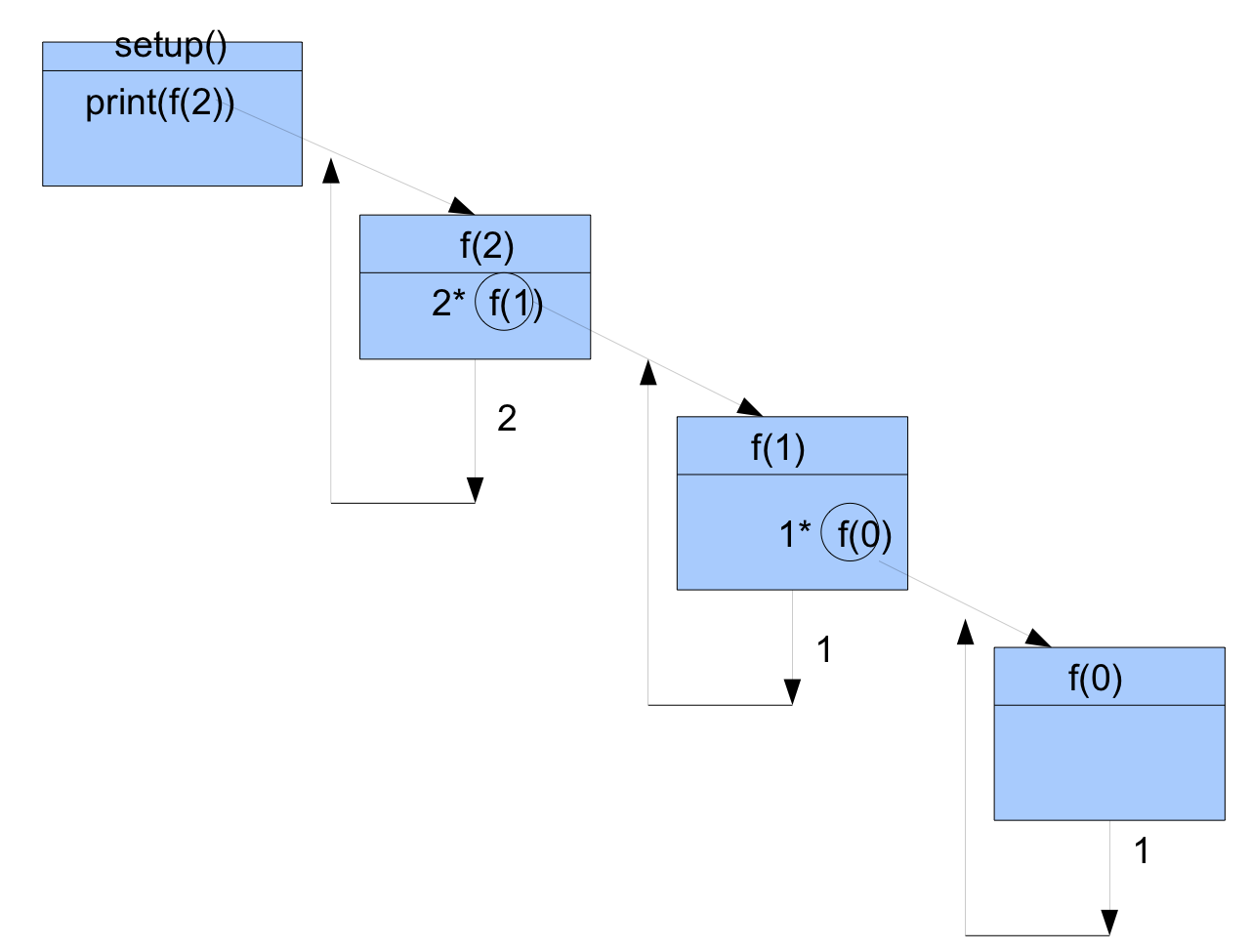
Lorsqu'on appelle la fonction factorielle(2), avant qu'elle n'ait retournée de valeur elle appelle à son tour la fonction factorielle(1) qui à son tour appelle la fonction factorielle(0)
La fonction factorielle(0) retourne la valeur 1 qui prend la place de factorielle(0) dans le corps de factorielle(1) qui va donc se terminer à son tour et retourner 1*1 = 1
Cette valeur 1 va prendre la place de factorielle(1) dans le corps de factorielle(2) qui va donc se terminer en retournant 2*1 = 2
Avantage et inconvénient de la programmation récursive
- Traduction quasiment immédiate d'un algorithme
- Appels répétés de la fonction pour les mêmes valeurs
Regardons cela sur l'exemple de la suite de Fibonnacci:
$u_n =u_{n-1}+u_{n-2}$ avec $u_0=u_1=1$
int fibonnacci(int n){
//Cas de base n = 1 ou n = 0
println("début de fibonnacci pour n = "+n);
if((n == 0) || (n == 1)){
println("fin de fibonnacci pour n = "+n);
return 1;
}
else{
int s = fibonnacci(n-1) + fibonnacci(n-2);
println("fin de fibonnacci pour n = "+n);
return s;
}
println("fin de fibonnacci pour n = "+n);
}
//-------------setup----------------
void setup(){
println("Fibonnacci de 5 vaut "+fibonnacci(5));
}
Recopiez et testez le programme ci-dessus
On constate (voir arbre ci-dessous) qu'on appelle plusieurs la fonction fibonnacci pour les mêmes valeurs, par exemple fibonnacci(2) est appelée 3 fois
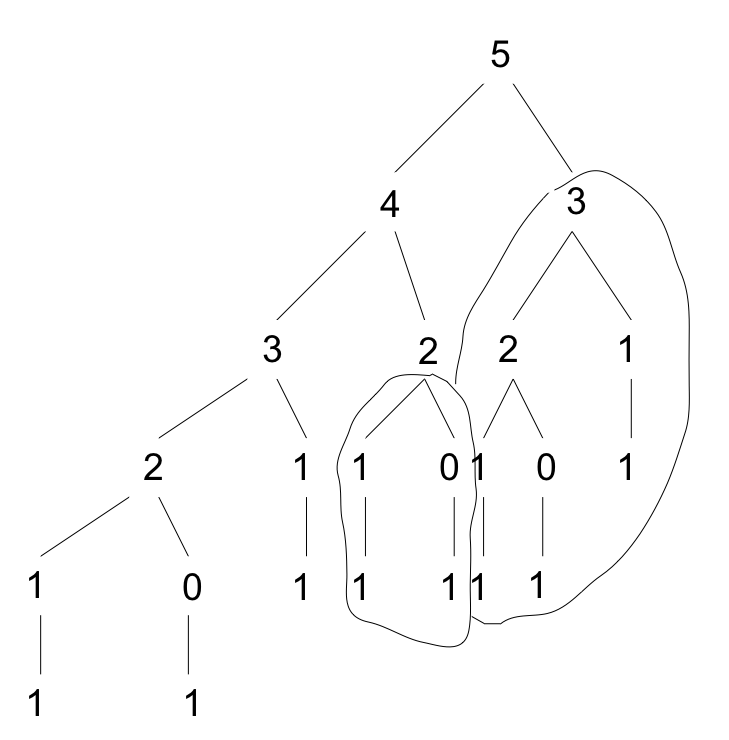
Pour éviter cela on va stocker dans une table les valeurs calculées et si une valeur est déjà stockée on retourne cette valeur (mémoïsation)
int[] tableValeurs =new int[5];
//--------------------------------------------------
int fibonnacciMemo(int n){
//Cas de base n = 1 ou n = 0
println("début de fibonnacci pour n = "+n);
if((n == 0) || (n == 1)){
println("fin de fibonnacci pour n = "+n);
return 1;
}
//n! = n * (n-1)!
else if(tableValeurs[n] != 0){
println("fin de fibonnacci pour n = "+n);
return tableValeurs[n];
}
else{
int s = fibonnacciMemo(n-1) + fibonnacciMemo(n-2);
println("fin de fibonnacci pour n = "+n);
//memoïsation
tableValeurs[n] = s;
return s;
}
}
//-------------setup----------------
void setup(){
println("Fibonnacci de 40 vaut "+fibonnacciMemo(40));
}
Recopiez et testez le programme ci-dessus pour calculer la valeur de la suite de Fibonnacci pour n = 20
Comparez les temps d'exécution des deux programmes en utilisant la fonction de Processing millis()
Programmation collective
Tours de Hanoï
8 disques sont empilés du plus grand au plus petit autour d'une tige verticale.Il s'agit de les déplacer sur une autre des deux autres tours en utilisant une tour intermédiaire

-
Pour comprendre le problème et trouver la nature récursive de ce problème, essayer avec 3 tours, noter les déplacements des disques et observer bien
De la gauche vers la droite on notera les axes 1,2 et 3 on notera les diamètres arbitraires des disques 6, 5 et 4
Supposons que l'on veuille déplacer les trois disques de l'axe 2 vers l'axe 1
On peut commencer par déplacer le sommet de la pile , le disque 4 vers l'axe 1, ce que l'on note 2 --> 1
Puis on peut faire 2 --> 3 , etc... Terminer
Regarder la suite des déplacements comme le parcours dans un arbre en profondeur, ce qui va nous aider à programmer la solution à ce problème de manière récursive
Créer une fonction récursive void hanoi(int a,int b,int n) où a et b peuvent prendre les valeurs 1 ou 2 ou 3 et n est le nombre de disques
Il faudra peut être mettre au point une fonction qui à partir de a et b donne l'axe auxiliaire c par exemple (1,2) --> 3 et (2,3) --> 1
Mini-projet personnel (avant J+7)
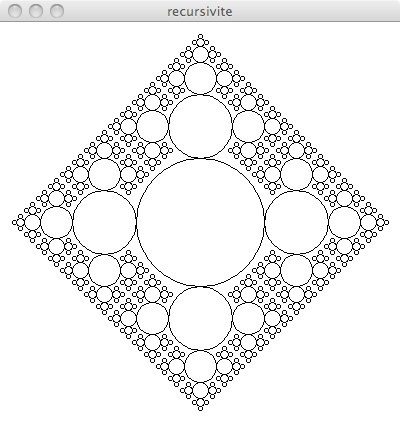
En vous aidant du manuel p 83 faire une fonction récursive qui réalise un dessin similaire au dessin suivant
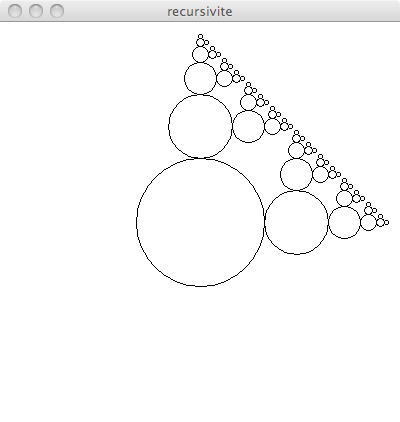
Puis du dessin suivant
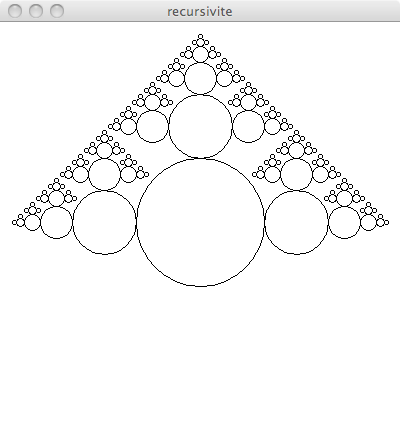
Puis du dessin suivant