Une IA pour le jeu du taquin

Le jeu du taquin

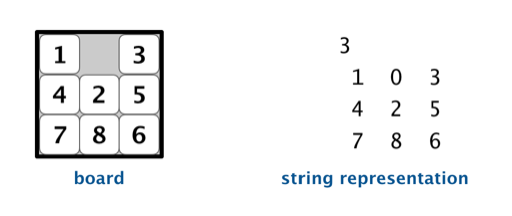
le jeu du taquin est constitué de 8 tuiles numérotées de 1 à 8 qui peuvent glisser verticalement ou horizontalement dans la direction de la place vide

Le but est de réarranger les tuiles dans l'ordre croissant,en partant de la situation initiale vers la situation finale comme on peut le voir ci-dessus

Le projet consiste à implémenter une IA pour un jeu du taquin ayant n*n - 1 tuiles pour n compris entre 2 et 128

Ce projet s'inspire d'un projet "Slider Puzzle" en Java de Sedgewick et Wayne

La classe Plateau

La classe Plateau est définie dans un fichier plateau.py

La classe Plateau modélise l'évolution du plateau de jeu

Voici l'API de la classe Plateau qu'il faudra implémenter en respectant les consignes ci-dessous

Toutes les méthodes devront être spécifiées et testées (avec doctest )

class Plateau:
    def __init__(self,n:int):
        """
        constructeur
        """
        pass
    def __str__(self)->str:
        """
        représentation du plateau
        """
        pass
    def hamming(self)->int:
        """
        distance de hamming
        """
        pass
    def manhattan(self)->int:
        """
        distance de manhattan
        """
        pass 
    def est_solution(self)->bool:
        """
        retourne vrai si le plateau est solution 
        """
        pass
    def est_egal(self,other)->bool:
        """
        retourne vrai si self est le même plateau que other
        """
        pass
    def voisins(self)->list:
        """
        retourne la liste des voisins de self
        """
        pass

1. Définir le constructeur

   le constructeur reçoit en paramètre n un entier égal au côté du plateau carré, avec 2 <= n <= 128

   Il faudra filtrer l'entrée du constructeur en gérant l'erreur si n n'est pas un entier vérifiant 2 <= n <= 128 (voir TP )

   La classe Plateau a deux attributs:

   • dimension qui récupère la valeur de n
   • tableau, un tableau 2D engendré par compréhension au hasard de n*n entiers entre 0 et n*n - 1

2. Définir la méthode __str__() qui donne une réprésentation du plateau sous forme d'une chaîne de caractères

   

3. La distance de manhattan entre deux points est la somme des décalages verticaux et horizontaux pour passer d'un point à l'autre

   Par exemple sur l'image ci-dessous la distance manhattan entre A et B est de 5

   

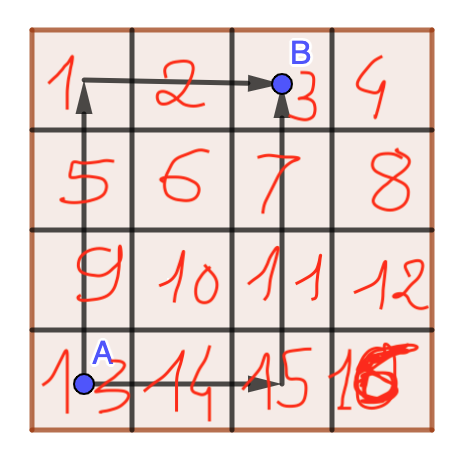
   Définir deux méthodes hamming() et manhattan() qui mesurent la distance entre le plateau actuel et la solution

   Pour définir ces distances nous avons besoin d'un repère, défini par la numérotation des cases du plateau par i + j*n + 1 avec i indice de ligne et j indice de colonne dans le tableau 2D tableaux2

   • la distance de hamming est le nombre de tuiles qui ne sont pas à leur place
   • la distance de manhattan est la somme des distances de manhattan de chaque tuile relativement à sa position dans la solution
4. Définir la méthode est_solution() qui retourne vrai si le plateau est une solution et faux sinon
5. Définir la méthode est_egal(other) qui retourne vrai si le plateau self est égal au plateau other (même dimension et mêmes éléments dans le tableau à deux dimensions)

6. Définir la méthode voisins() qui retourne la liste des plateaux voisins du plateau self

   Suivant la position de l'emplacement vide un plateau a 2, 3 ou 4 voisins

Permutations

Pour définir l'IA nous avons besoin d'un outil appelé permutation

Regardons les tuiles comme des personnes dans une pièce à qui on demande de se déplacer pour arriver à la solution

On choisit un repèrage absolu (peut-on faire un repèrage relatif ?)

Ou encore imaginons que l'on peut "libérer" les tuiles de toute contrainte de déplacement, ainsi la façon la plus rapide de passer de l'état actuel du plateau à la solution est

• La tuile 1 qui est en position 2 dans le repère va en position 1 on note cela 2 -> 1
• 5 -> 2
• 6 -> 5
• 0 -> 6
• 1 -> 0
• Les autres tuiles ne bougent pas

On note le tableau de valeurs de cette fonction p de déplacement relativement au repère choisi sous cette forme

 0 1 2 3 4 5 6 7 8 
 6 0 1 3 4 2 5 7 8 

ce qui signifie p(1) = 0, p(2) = 1, etc...

Orbites d'une permutation

Pour comprendre ce que signifie cette notion regardons les images successives de 1

1 -> 0 -> 6 -> 5 -> 2 -> 1

On revient ensuite en 1

On dit qu'on a une permutation circulaire qu'on note (1 9 6 5 2) et on dit qu'elle a pour longueur 5

Autrement dit on peut écrire p = (1 0 6 5 2) = (0 6 5 2 1)

Peut on savoir uniquement à partir de cette information qu'il y a une solution? Comment trouver la suite de coups de la solution ?

Signature d'une permutation

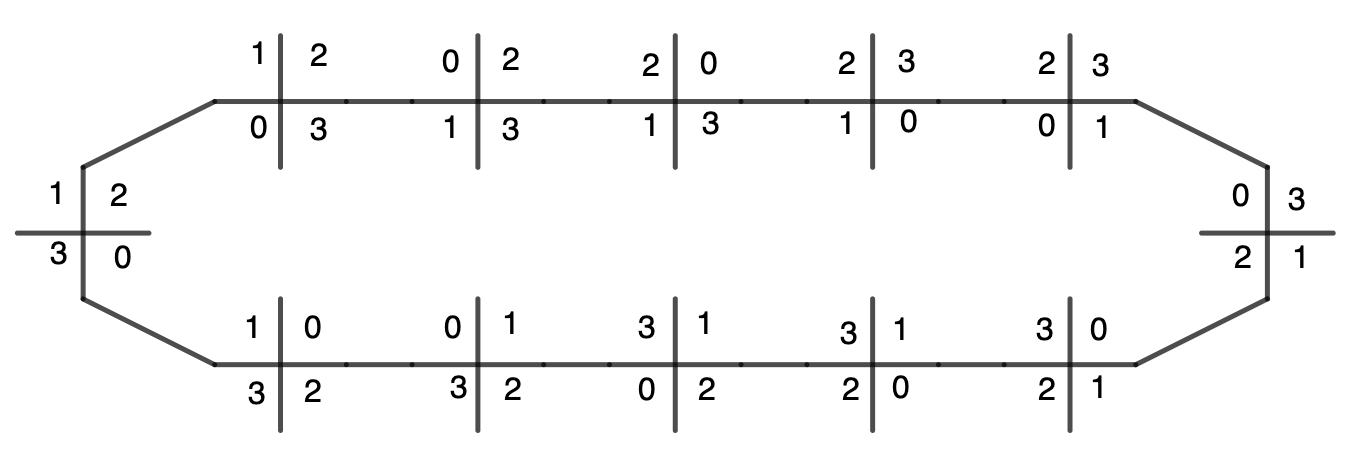
On transforme le plateau de jeu en une file comme expliqué dans l'article suivant

On a disposé la file de telle sorte que tout déplacement d'une tuile vers la case vide qui n'est pas dans le sens de la file fait "gagner ou perdre un nombre pair de places" à cette tuile dans la file

Il y a donc un invariant pour n'importe quel mouvement sur le plateau, c'est la parité du nombre d'inversions

Un plateau donné pourra être transformé en plateau solution si le nombre d'inversions associé à chaque file a la même parité

1. Définir une fonction Python récursive nb_inversions(liste:list) qui renvoie le nombre d'inversions d'une liste d'entiers
2. Définir une fonction a_solution(plateau:list,dim :int ) qui renvoie Vrai si le plateau conduit à une solution Faux sinon

Graphe du jeu de taquin

Pour n = 2 il y a 4! = 24 dispositions différentes pour le plateau et chaque configuration a exactement deux voisins dans le graphe du jeu

File de priorité min

Les observations précédentes nous donnent l'idée d'un algorithme pour une IA pour le jeu du taquin