Algorithmique

Les bibliothèques matplotlib et numpy

Nous allons tracer des graphes pour illustrer la complexité de certains algorithmes

Pour cela nous allons utiliser les bibliothèques numpy et matplotlib

Questions

  1. Aller sur le site de matplotlib

  2. Copier le code suivant et le coller dans l'éditeur de wingIDE ou Edupython

    En cliquant dans le code sur la page de matplotlib comprendre le code ci-dessous

    
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 2, 100)

plt.plot(x, x, label='linear')
plt.plot(x, x**2, label='quadratic')
plt.plot(x, x**3, label='cubic')

plt.xlabel('x label')
plt.ylabel('y label')

plt.title("Simple Plot")

plt.legend()

plt.show()

Complexité de la recherche séquentielle d'une valeur dans un tableau

Il s'agit de tracer la courbe du temps d'exécution de la recherche séquentielle d'un élément placé en dernière position dans une liste pour différentes tailles de listes

Questions

  1. Copier le code suivant et l'exécuter

    Ce code mesure le temps en secondes d'exécution de la fonction estDansTableau(999,liste)

       	
   	import time
   	
   	def estDansTableau(val,liste):
   	    for elt in liste:
   	        if elt == val:
   	            return True
   	    return False
   	     
   	 liste = [i for i in range(1000)]
   	 t1 = time.time()
   	 estDansTableau(999,liste)
   	 t2 = time.time()
   	 print(t2 - t1)

  2. Créer une liste tailles en compréhension de 10000 à 10 millions (suite géométrique de raison 10)
  3. Créer une fonction mesurerTemps(tailles) qui retourne une liste contenant les temps d'exécution de la recherche séquentielle de la valeur tailles[i] - 1 dans le tableau de 1 à tailles[i] - 1
  4. Ensuite tracer: 
       	 
   	 tailles = [10**k for k in range(4,8)] 
     plt.plot(tailles,mesurerTemps(tailles))
     plt.show()

    on obtient cela

Nombres d'occurences

  1. Télécharger le fichier texte suivant Vibrio_cholerae.txt contenant la séquence génomique d'une des bactéries transmettant le choléra
  2. Ecrire une fonction Python qui lit le fichier texte et retourne un tuple formé du nombre de lettres A,C,G et T contenues dans la séquence génomique de la bactérie
  3. La taille du fichier est de 1,1 Mo, cela correspond-t-il au nombres de nucléotides contenus dans la séquence génomique ?

Hauteur maximale de vagues

Des balises sont placées à divers endroits des océans pour mesurer à chaque heure la température de l'eau, la vitesse du vent la hauteur des vagues etc... Les balises maritimes M4 (irlandaise , celle qui est la plus proche de l'Irlande) et K5(anglaise) (encerclées sur la carte) ont mesurées ces dernières années les plus hautes hauteurs de vagues dans le monde. A l'aide du fichier csv de 9 Mo contenant les données horaires de la balise M4 de 2002 jusqu'à maintenant (2019) il s'agit de trouver la plus haute hauteur de vague mesurée par cette balise et quand elle a été mesurée

  1. A l'aide d'un éditeur de texte ouvrir le fichier hly62093.csv et répondre aux questions suivantes
  2. En quelle unité est mesurée la hauteur de vague ?
  3. A partir de quelle année les données sont significatives?
  4. Dans quel champ se trouve la hauteur de vague significative (waht)?
  5. Comprendre la fonction python rechercheMaxHauteurVague() pour la faire évoluer de telle sorte qu'elle retourne un tuple composé de la date et de la hauteur de vague maximale 
    
def maxHauteurVague():
    import csv
    h_max = 0
    with open("hly62093.csv","r") as fichier:
        reader = csv.reader(fichier)
        compteur = 0
        for ligne in fichier:
            compteur = compteur + 1
            if compteur > 20 :
                chaine = ligne.split(",")[9]
                if chaine != ' ':
                    val = float(chaine)
                
                    if val > h_max:
                        h_max = val
            
    return h_max

Complexité du tri par sélection

Il s'agit de tracer la courbe du temps d'exécution du tri par sélection d'une liste pour différentes tailles de listes

Questions

    Ecrire en python la fonction triSelection(liste)

    Du module random importer la fonction shuffle() qui mélange aléatoirement une liste

    Procéder comme la recherche séquentielle pour tracer une courbe du temps d'exécution en fonction de différents tailles de liste

  1. Créer un tableau tailles en compréhension de 10000 à 10 millions (suite géométrique de raison 10)
  2. Créer une fonction mesurerTemps(tailles) qui retourne un tableau contenant les temps d'exécution du tri par sélection dans le tableau de 1 à tailles[i] - 1
  3. Ensuite tracer: 
       	 
   	 tailles = [10**k for k in range(2,5)] 
     plt.plot(tailles,creeMesures(tailles))
     plt.show()

Complexité du tri par insertion

Il s'agit de tracer la courbe du temps d'exécution du tri par sélection d'une liste pour différentes tailles de listes

Questions

    Ecrire en python la fonction triSelection(liste)

    Du module random importer la fonction shuffle() qui mélange aléatoirement une liste

    Procéder comme la recherche séquentielle pour tracer une courbe du temps d'exécution en fonction de différents tailles de liste

  1. Créer un tableau tailles en compréhension de 10000 à 10 millions (suite géométrique de raison 10)
  2. Créer une fonction mesurerTemps(tailles) qui retourne un tableau contenant les temps d'exécution du tri par sélection dans le tableau de 1 à tailles[i] - 1
  3. Ensuite tracer: 
       	 
   	 tailles = [10**k for k in range(2,5)] 
     plt.plot(tailles,creeMesures(tailles))
     plt.show()

Preuve de programme

A travers un exemple on découvre l'idée de preuve de programme

Théorème de la division euclidienne : Etant donné un entier naturel $a$ et un entier naturel $b > 0$, il existe un entier naturel unique $q$ et un entier naturel $r$ unique tel que $a = bq +r $ avec $0 \leqslant r < b$

Nous allons prouver ce théorème de manière algorithmique

L'idée consiste à retrancher à a autant de fois que c'est possible b jusqu'à ce que le résultat soit dans l'intervalle [0,b[

Et prouver le théorème équivaut à prouver le programme ci-dessous

Prouver le programme revient à montrer que si la précondition est vraie et si le programme s'exécute et se termine alors la postcondition sera vraie aussi

  
  div(a,b)
  
  Données (ou précondition): a entier >= 0, b entier > 0
  Résultat (ou postcondition): q entier >= 0, r entier >= 0 tel que a = bq + r et r < b
  
      r <- a
      q <- 0
      {r = a - bq}
      Tant que r >= b faire
          q <- q + 1
          r <- r - b
          {r = a - bq}
      retourner q,r

En algorithmique on dit que {r = a - bq} est une assertion, autrement dit une relation vraie entre des variables, à un moment donné du programme

De manière générale on peut regarder la preuve d'un programme P comme une déduction passant de la {Précondition} à la {Postcondition} en passant par P

La difficulté de la déduction vient de la présence d'une boucle dans le programme

L'Heuristique est de chercher un invariant de boucle, c'est à dire une assertion vraie au début de la boucle et qui reste vraie après à chaque itération

En général l'invariant de boucle est en rapport avec la solution du problème

Preuve que I(r,q) = {r = a - bq} est un invariant de boucle

Vrai à l'entrée de la boucle en effet le contenu de r vaut a celui de q vaut 0 donc le test d'égalité r = a - bq retourne vrai

Supposons que la propriété est vraie à la fin de plusieurs tours de boucles (instant t) et que l'on fait un tour de boucle supplémentaire . (instant t' > t)

Notons $q$ et $r$ les contenu des variables $q$ et $r$ à l'instant t, et $q'$ et $r'$ à l'instant t'

L'expression $r = a - bq$ est vraie à l'instant t or $r'$ vaut $r-b$ et $q'$ vaut $q+1$ donc $a -bq'$ vaut $a - b(q+1) = a -bq -b= r-b = r'$

Donc l'expression $r = a - bq$ est vraie à l'instant t'

Preuve de la terminaison de la boucle

Pour prouver qu'une boucle se termine il faut chercher une grandeur strictement monotone (un variant de boucle) ici $r$ qui est strictement décroissant et qui finira par être strictement plus petit que $b$

Déduction de la postcondition

Pour simplifier Précondition + Invariant de boucle + Terminaison -> Postcondition

En effet à la sortie de la boucle $0 \leqslant r < b$ mais d'après l'invariant de boucle $r = a-bq$ donc $a = bq +r$ avec $0 \leqslant r < b$

En Python on peut mettre des assertions qui bloquent l'exécution du programme si l'expression est fausse, on peut tester ainsi la précondition, l'invariant de boucle et même ici la postcondition

  
  def div(a,b):
  
  """paramètres:  a entier >= 0, b entier > 0
  
     Résultat: q entier >= 0, r entier >= 0 tel que a = bq + r et r < b
  """
      assert(isinstance(a,int))
      assert(isinstance(b,int) and b > 0)
      r = a
      q = 0
      assert(r == a - bq)
      while r >= b :
          q = q + 1
          r = r - b
          assert(r == a - bq)
      assert(q == a //b)
      assert(r == a % b)
      return q,r

Recherche dichotomique

Il s'agit de vérifier expérimentalement la complexité de la recherche dichotomique comparée à celle de la recherche séquetielle

Questions

    Ecrire en Python la fonction estDansTableauDicho(v,liste)

    Procéder comme la recherche séquentielle pour tracer une courbe du temps d'exécution en fonction de différents tailles de liste

  1. Créer un tableau tailles en compréhension de 10000 à 10 millions (suite géométrique de raison 10)
  2. Créer une fonction mesurerTemps(tailles) qui retourne un tableau contenant les temps d'exécution du tri par sélection dans le tableau de 1 à tailles[i] - 1
  3. Ensuite tracer: 
       	 
   	 tailles = [10**k for k in range(2,5)] 
     plt.plot(tailles,creeMesures(tailles))
     plt.show()

Rendu de monnaie (stratégie gloutonne)

Dans un algorithme glouton il existe un ensemble ordonné dans lequel à chaque itération on prend le plus grand ou le plus petit élément de cet ensemble et on l'exclut de cet ensemble pour diminuer le nombre de possiblités (variant de boucle)

Comment va-t-on faire cela en Python pour le problème de rendu de monnaie ?

Il existe une fonction en Python associée aux listes qui permet à la fois de prendre l'élément ayant le plus grand indice dans une liste et enlever cet élément de la liste, c'est la fonction pop()

Dans une console Python exécuter les instructions suivantes

Vous pouvez observer que la fonction pop() appliquée à la liste p = [1, 2, 5, 10] permet de récupérer l'élément 10 puis la liste devient p = [1,2,5]

Copier-Coller le code suivant et l'exécuter pour 43 euros et 72 euros



PIECES = [1,2,5,10]

def div(a,b):
    """
    retourne le quotient et le reste de la division euclidienne de a par b 
    
    paramètres:
    ----------
    a : int
       entier naturel
    b : int
       entier naturel > 0
 
    résultat:
    ---------
    tuple
        le quotient et le reste de la division euclidienne de a par b 
    """
    return a // b, a % b

def renduMonnaie(somme):
    """
    retourne le nombre de chaque type de pièces 
    où le système de pièces est PIECES = [1,2,5,10] 
    
    paramètres:
    ----------
    somme : int
       une somme en euros
    
    résultat:
    ---------
    list
        la liste du nombre de chaque type de pièces 
    """
    p = PIECES
    s = somme
    rendu = [0]*4
    i = 3
    while s > 0:
        val = p.pop()
        nbPieces,s = div(s,val)
        rendu[i] = nbPieces
        i = i - 1
    return rendu
    
print(renduMonnaie(43))

On généralisera en Terminale, grâce à la programmation objet, la notion de liste par la notion de structure, de telle sorte que l'on puisse créer des fonctions insérer un élément dans une structure et aussi enlever un élément dans une structure, facilement dans un programme

Plus court chemin dans un graphe (Algorithme de Dijkstra)

On appelle graphe, un ensemble de sommets, ici les éléments 0, 1, 2, 3 et 4 et d'arêtes (les flèches) reliant certains éléments entre eux

Ces arêtes sont orientées ainsi il y a une arête qui part de 0 vers 1, et valuées avec des nombres positifs par exemple, l'arête qui part de 0 vers 1 a pour valeur 50

On peut imaginer qu'un tel graphe peut représenter les temps de transport entre les différentes stations de métro d'une ville

Un des sommets est l'origine ou la source (on choisit ici le sommet 0)

Le but du problème est de trouver les valeurs des plus courts chemins entre la source et les autres sommets

Pour cela on dispose du tableau D = [50, 30, 100, 10] donnant dans l'ordre les distances de 0 à 1, puis de 0 à 2, puis de 0 à 3 et enfin de 0 à 4

Ce tableau va évoluer tout au long de l'exécution de l'algorithme car on va trouver une distance plus courte pour aller de 0 à 4

L'équivalent de l'ensemble des pièces est ici l'ensemble des sommets différents de la source 0, c'est à dire C = [1,2,3,4]

  1. On cherche le sommet le plus proche de la source pour les éléments de C: C'est le sommet 4, on l'enlève de l'ensemble C, donc C devient [1,2,3] et on regarde maintenant si on peut faire mieux dans le tableau D, en passant par le sommet 4 pour aller vers 1, 2 ou 3

    Oui car le chemin 0-4-3 prend moins de temps que 0-3 donc on remplace 100 par 10 + 10 = 20 et D = [50,30,20,10]

  2. On cherche encore le sommet le plus proche de la source pour les éléments de C: C'est le sommet 3, on l'enlève de l'ensemble C, donc C devient [1,2] et on regarde maintenant si on peut faire mieux dans le tableau D, pour aller de la source vers 1, 2 via le sommet 3

    Oui car le chemin 0-4-3-1 prend moins de temps que 0-1 donc on remplace 50 par 20 + 20 = 40 et D = [40,30,20,10]

  3. On cherche encore le sommet le plus proche de la source pour les éléments de C: C'est le sommet 2, on l'enlève de l'ensemble C, donc C devient [1] et on regarde maintenant si on peut faire mieux dans le tableau D, pour aller de la source vers 1 via le sommet 2

    Oui car le chemin 0-3-1 prend moins de temps que 0-1 donc on remplace 40 par 30 + 5 = 35 et D = [35,30,20,10]

Copier le code suivant et compléter la fonction minimum(candidats,distances)

Exécuter le


from math import inf

def minimum(candidats,distances):
    """
    retourne le candidat le plus proche de la source relativement au tableau
    distances  
    
    paramètres:
    ----------
    candidats : list
       un sous ensemble de sommets du graphe
    distances : list
       les distances de la source vers les candidats
 
    résultat:
    ---------
    int
        le candidat le plus proche de la source 
    """
    pass
    

def dijkstra(L,source):
    """
    retourne la liste des distances les plus petites
    de la source aux autres sommets du graphe
    
    paramètres:
    ----------
    L : list
       une liste de liste des distances entre les sommets
    source : int
       un des sommets du graphe
    résultat:
    ---------
    list
        la liste des distances les plus petites de la source aux autres sommets 
    """
    nbSommets = len(L[0])
    #On initialise la liste des candidats
    #Ce sont tous les sommets sauf la source
    candidats = [i for i in range(nbSommets)]
    candidats.remove(source)
    
    #A l'état initial la liste distances contient les distances
    de la source à tous les autres sommets
    distances = L[source]
    
    #on visite chaque candidat le plus prometteur, au sens
    #où sa distance à la source est la plus petite
    #relativement à la liste distances régulièrement mis à jour
    #après chaque itération
    for i in range(nbSommets - 2):
        v = minimum(candidats,distances)
        candidats.remove(v)
        for elt in candidats:
            distances[elt] = min(distances[elt],distances[v] + L[v][elt])
    return distances
        
L = [ [inf,50,30,100,10],
      [inf, inf, inf, inf, inf],
      [inf, 5, inf, 50, inf],
      [inf, 20, inf, inf, inf, inf],
      [inf, inf, inf, 10, inf]]  
print(dijkstra(L,0))

Coloration d'un graphe

Exercice

  1. Colorier le graphe suivant "à la main" avec l'algorithme glouton vu en cours

    Vous avez utilisé 2 couleurs n'est ce pas ?

  2. Colorier le graphe suivant "à la main" avec l'algorithme glouton vu en cours

    Cette fois ci vous avez utilisé 3 couleurs, n'est ce pas ?

  3. Maintenant il s'agit d'implémenter l'algorithme

    D'abord on va représenter le dernier graphe par une liste de listes [[4],[2,3],[1,4],[1,4],[0,2,3]] où chaque liste est la liste des voisins du sommet d'indice i

    Ainsi le sommet d'indice 0 a pour liste de voisins [4], et on voit sur le dessin que le sommet 0 a un seul voisin le sommet 4

    Ainsi le sommet d'indice 1 a pour liste de voisins [2,3], et on voit sur le dessin que le sommet 1 a pour voisins les sommets 2 et 3

  4. Pour voir si vous avez compris faites la liste correspondant au premier graphe

Maintenant on va implémenter l'algorithme, copier le code suivant et le compléter (voir plus loin les consignes)

    
NB_SOMMETS = 5

def plusPetiteCouleurNonAttribuee(voisins,couleur):
    """
    retourne lea plus petite couleur non attribuée aux voisins du sommet
    
    paramètres:
    ----------
    voisins : list
                liste d'entiers (les voisins d'un sommet)
    couleur : list
                liste d'entiers (les couleurs attribuées ou pas encore à
                tous les sommets du graphe
 
    résultat:
    ---------
    int
        le plus petit entier supérieur ou égal à 0 non attribué aux voisins
    
    """
    couleurs_utilisees = [False]*len(voisins)
    for voisin in voisins:
        if couleur[voisin] != -1:
            ....... à compléter .........
    for i in range(len(couleurs_utilisees)):
        if ..............:
            return i 
            
def colorieGraphe(graphe):
    """
    colorie le graphe par une méthode glouton
    
    paramètres:
    ----------
    graphe : list
                liste de liste de voisins des sommets du graphe
 
    résultat:
    ---------
    list
        la liste des couleurs des sommets
    
    """
    couleur_sommet = [-1]*NB_SOMMETS
    couleur_sommet[0] = 0
    for i in range(1,len(graphe)):
        #parcourir les voisins de i
        couleur_sommet[i] = plusPetiteCouleurNonAttribuee(graphe[i],couleur_sommet)
    return couleur_sommet

def nbCouleursUtilisees(couleurs):
    """
    retourne le nombre de couleurs utilisées pour colorier le graphe
    
    paramètres:
    ----------
    couleurs : list
                liste des couleurs des sommets
 
    résultat:
    ---------
    int
        le nombre de couleurs
    
    """
    pass 
    
 #-----------------------------main---------------------------- 
graphe = [[4],[2,3],[1,4],[1,4],[0,2,3]]

couleurs = []

couleurs = colorieGraphe(graphe)

print(couleurs)

print("Le nombre de couleurs utilisées est ",nbCouleursUtilisees(couleurs))

    1. Il s'agit de compléter la fonction plusPetiteCouleurNonAttribuee(voisins,couleur)

      Un tableau de booléens couleurs_utilisees mémorise les couleurs utilisées pour tous les sommets, ce tableau est initialisé qu'avec des False

      On utilisera la convention suivante si une couleur n'est pas encore attribuée à un sommet, la couleur du sommet est -1

      Si un voisin est coloré par une couleur k il faut mettre True dans le tableau couleurs_utilisees à l'indice k

      Ensuite on parcourt le tableau couleurs_utilisees et on retourne l'indice i du premier False rencontré

    2. Il n'y a rien à compléter dans la fonction colorieGraphe(graphe), qui est la traduction en Python de l'algorithme vu en cours
    3. Définir la fonction nbCouleursUtilisees(couleurs) qui retourne le nombre de couleurs utilisées pour colorier le graphe
    4. Exécuter le programme, avez vous trouvé le même résultat que celui obtenu dans l'exercice ?
    5. Relancer le programme pour le premier graphe

Algorithme du plus proche voisin

Exercice

  1. Télécharger le squelette du code
  2. Télécharger le fichier iris.csv (ces deux fichiers doivent se trouver dans le même dossier)
  3. Avec un éditeur de texte ouvrir le fichier iris.csv, et observer les descripteurs (première ligne) (on travaillera avec les champs d'indice 2, 3 et 4)

  4. Renommer le fichier kpp_sequelette.py, kpp.py et exécuter le,vous devez observer la base d'apprentissage constituée de la moitié des données

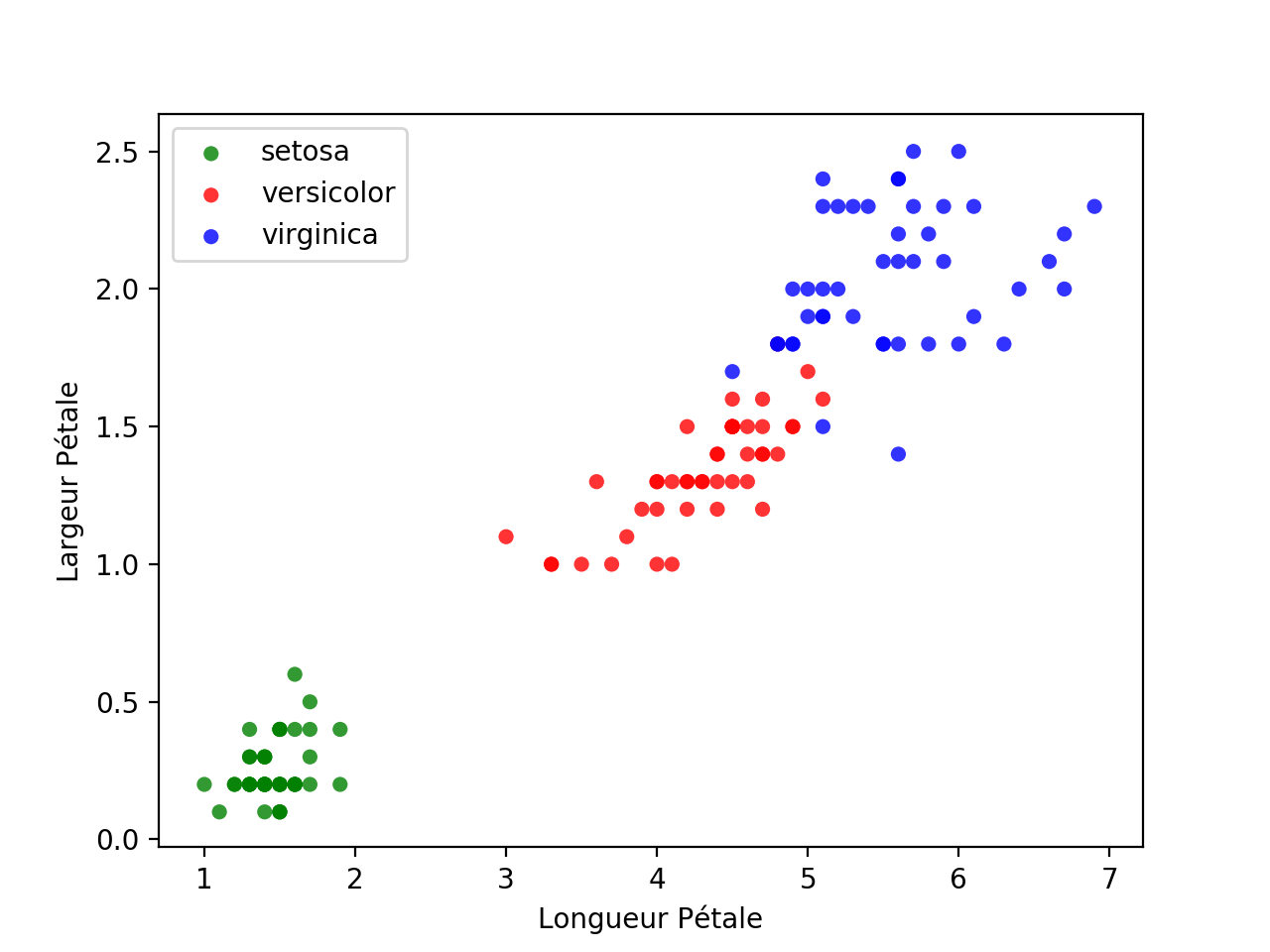
    L'autre moitié des fleurs dont on connaît pourtant la classe, 'setosa', 'versicolor' ou 'virginica', servira de base de test pour notre algorithme

    L'algorithme du plus proche voisin a été exécuté mais à l'affichage on n'a pas sa mesure de performance

    Il vous reste à mettre au point cette fonction,cependant pour se faire il vous faudra utiliser une fonction très pratique en Python la fonction zip qui permet de parcourir deux listes en même temps (le zip de la fermeture éclair)

    Copier le code suivant exécuter le puis s'en inspirer pour mesurer coder la performance de l'algorithme du plus proche voisin

    
prenoms = ['Jacques','Paul','Claire']
noms = ['Celler','Hisse','Aubescure']
for identite in zip(prenoms,noms)
    print(identite)

    A l'exécution vous devez observer que la mesure de performance vaut 0.92

  5. Maintenant il s'agit de finir de mettre au point l'algorithme des k plus proches voisins

    Dans le main commenter la ligne

    fleurs_classees = ppv(fleurs_app,fleurs_test)

    Puis décommenter les deux lignes

    #k = 3

    #fleurs_classees = kppv(fleurs_app,fleurs_test,k)

    En vous aidant du cours (pdf disponible sur Pronote) mettre au point les fonctions insertion(d,b,d_min,b_min,k) et classe_majoritaire(b_min,k)

    A l'exécution vous devez obtenir cette fois-ci une mesure de performance de 0.97