Arbre binaire de recherche

Classe ABR

def ajouter(arbre,valeur):
    if arbre is None:
        return Noeud(valeur,None,None)
    if valeur < arbre.valeur:
        return Noeud(arbre.valeur,
        ajouter(arbre.gauche,valeur),arbre.droit)
    elif valeur > arbre.valeur:
        return Noeud(arbre.valeur,arbre.gauche,
        ajouter(arbre.droit,valeur))
    else:
        return arbre

def rechercher(arbre,valeur):
    if arbre is None:
        return False
    if valeur < arbre.valeur:
        return rechercher(arbre.gauche,valeur)
    elif valeur > arbre.valeur:
        return rechercher(arbre.droit,valeur)
    else:
        return True




class ABR:
    def __init__(self):
        self.racine = None

    def ajouter(self,val):
        self.racine = ajouter(self.racine,val)

    def rechercher(self,val):
        return rechercher(self.racine,val)

Ajouter les méthodes suivantes

• hauteur()
• valeur_max()
• valeur_min()
• supprime_max()

Pour visualiser l'arbre utiliser graphviz comme au TP sur les arbres

Equilibre d'un ABR

Un arbre binaire de recherche dégénéré de n sommets a une taille de n et une hauteur de n aussi

Un arbre binaire de recherche complet de taille $2^{n} - 1$ a une hauteur $n$

Le quotient, appelé ici coefficient d'équilibre, $\dfrac{\ln_2(n+1)}{h}$ mesure le fait qu'un arbre binaire de recherche soit plus ou moins complet, donc plus ou moins "équilibré" et varie entre 1 le maximum pour un arbre complet et parfaitement équilibré et $\dfrac{\ln_2(n+1)}{n}$ le minimum pour un arbre dégénéré donc le plus déséquilibré possible

• Ajouter un attribut taille à un objet ABR et modifier les méthodes ajouter() et supprime_max()
• Ajouter une méthode coefficient_equilibre()
• En utilisant la méthode shuffle de la bibliothèque random générer des arbres binaires de recherche aléatoires de taille 100
• Visualiser avec graphiz

• Observer l'évolution du coefficient d'équilibre lorsque on ajoute 20 valeurs supplémentaires au hasard et qu'on utilise 20 fois la méthode supprime_max()

Tas

Un arbre binaire de recherche peut être redéfini comme un arbre binaire ordonné horizontalement.

Qu'est ce qu'un arbre binaire orienté verticalement ?

Un arbre binaire est orienté verticalement si pour tout noeud autre qu'une feuille la valeur de ce noeud est inférieur à celle de ses deux fils.

Un arbre binaire est essentiellement complet si tous les niveaux sont complets à part le dernier peut-être et toutes les feuilles sont tassées à gauche.

Un tas min T est un arbre binaire essentiellement complet orienté verticalement.

Un tas max T est un arbre binaire essentiellement complet vérifiant:

Pour tout noeud i : T[parent(i)] >= T[i]

En conséquence contrairement aux arbres binaires de recherche les valeurs des sous arbre gauche et sous arbre droit d'un noeud sont inférieures ou égales à la valeur du noeud.

De plus le plus grand élément du tas max est la racine de l'arbre.

Pourquoi s'intéresser aux tas ?

• Un tableau suffit pour mémoriser le tas.
• Un tas permet de gérer une grande quantité de données qu'on ne peut pas stocker dans son ensemble mais seulement les plus grandes valeurs (tas max) ou les plus petites valeurs (tas min).
• Un tas permet de créer une file de priorité (utile dans les systèmes d'exploitation, routeurs,algorithmes de Dijkstra).

Exemple

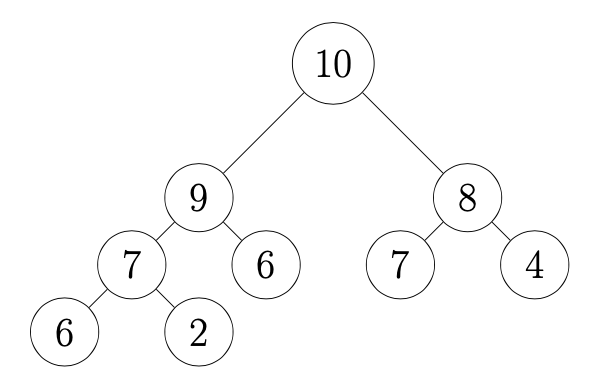
On range les valeurs d'un tas dans un tableau T ainsi :

Dans T[0] on met la taille de l'arbre

Pour un noeud i rangé dans T[i], le fils droit est rangé dans T[2*i] le fils gauche dans T[2*i +1]

Pour un noeud i rangé dans T[i], son père est rangé en T[i//2].

On veut implémenter une classe Tas_max avec les méthodes suivantes :

On crée un tas vide mais de taille n,puis ensuite :

• On crée le tas en insérant les valeurs une par une grâce à une méthode inserer(val)

• On créé le tas à partir d'une liste d'entiers de taille n.

  Comment ?

  Un tas mémorisé dans un tableau a une propriété intéressante:

  Les noeuds qui ne sont pas des feuilles ont leur indice compris entre 1 et n//2 (Justifier)

  Une feuille dans la liste est forcément bien placée, par contre l'élément d'indice n//2 est peut-être trop petit et il faut le faire descendre à sa place dans le tas max, on va implémenter une fonction tamiser(i) pour faire ce travail.

  Donc pour créer le tas max à partir de la liste il suffit de tamiser les éléments de l'indice n//2 à 1.

Voici l'interface d'un Tas_max

    
def echanger(valeurs:list,i:int,j:int)->None:
    temp = valeurs[i]
    valeurs[i] = valeurs[j]
    valeurs[j] = temp

def max_fils(tableau:list,i:int,taille:int)->int:
    """
    renvoie l'indice 2*i ou 2*i+1 de la plus grande valeur
    de l'un des deux fils du noeud i dans un tas max
    Attention ! risque de "index out of range"
    lorsqu'on arrive au dernier niveau du tas
    lorsque t[2i] existe mais pas forcément t[2i+1]
    """
    ind_max = i << 1
    if .....:
        return .....
    return ind_max

class Tas_max:
    """
    un tas max T de taille n
    vérifie pour 1 <= i <= n     T[parent(i)] >= T[i]
    On implémente un Tas dans une liste
    fils_gauche(i) = 2*i et fils_droit(i) = 2*i + 1
    parent(i) = i//2
    On peut construire un Tas max soit en ajoutant élément par élément
    à partir d'un tas vide:
    ->inserer(val)
    on peut aussi construire un tas max directement à partir
    d'un valeursleau de taille n:
    ->cree_tas_max(valeursleau)
    """

    def __init__(self,n=0):
        """
        n = 0 si on cree un tas max vide
        sinon n est la taille du valeursleau
        à partir duquel on crée le tas max
        """
        self.taille = n
        self.valeurs = [n]

    def inserer(self,val:int)->None:
        """
        permet d'insérer une valeur val au bon endroit dans
        un tas max
        On insère la valeur val à la fin du tas et on remonte (percoler)
        cette valeur dans le tas
        """
        self.taille += 1
        self.valeurs[0] += 1
        self.valeurs.append(val)
        self.percoler(self.taille)

    def tamiser(self,i:int)->None:
        """
        la valeur du noeud i est  strictement plus petite
        que l'un de ses enfants
        On fait descendre cette valeur dans l'arbre jusqu'à ce
        qu'elle trouve sa place
        complexité logarithmique
        """
        pass

    def percoler(self,i:int)->None:
        """
        La valeur du sommet i est strictement plus grande
        que celle de son parent.
        On fait monter cette valeur dans l'arbre
        jusqu'à ce qu'elle retrouve sa place
        """
        pass

    def maximum(self)->int:
        """
        renvoie la valeur de la racine du tas max
        qui est le maximum du tas
        """
        return self.valeurs[1]

    def cree_tas_max(self,tableau):
        """
        cree un tas max de n éléments à partir d'un tableau de n éléments
        Propriété : les feuilles d'un arbre binaire complété sont indexés par
        E(n/2) + 1, E(n/2) + 2,...,n
        Autrement dit ça ne sert à rien de tamiser les feuilles
        On tamise les noeuds qui ne sont pas des feuilles dans l'ordre inverse
        de E(n/2)  jqà la racine
        complexité linéaire
        """
        for i in range(self.taille):
            self.valeurs.append(tableau[i])
        for i in range(self.taille//2,0,-1):
            self.tamiser(i)

    def supprime_racine(self)->int:
        """
        on échange la racine et la dernière valeur du tas
        on tamise la nouvelle racine
        on retourne la dernière valeur
        on enlève de la liste la dernière valeur
        complexité logarithmique
        """
        pass

    def __str__(self):
        ch = ""
        for i in range(1,self.taille+1):
            ch += " | "+str(self.valeurs[i])
        ch += " |"
        return ch

def tri_tas(tableau:list)->list:
    """
    à partir d'un Tas max on trie dans l'ordre croissant
        Tas max
    idée:
    échange le maximum (la racine) et le dernier élément
    Tamise la racine
    échange la racine avec l'avant dernier etc..
    """
    pass
    
    

• Implémenter les méthodes manquantes, pour la méthode tamiser(i) il faut implémenter la fonction max_fils(tableau,i,taille)
• Implémenter la fonction tri_tas(tableau)

File de priorité

On crée une classe de tâches domestiques nommée Tache ayant deux attributs

• nom : une chaîne de caractères, décrivant la tâche
• cle : un entier entre 1 et 10, mesurant la priorité de la tâche, plus ce nombre est grand plus la tâche est prioritaire

Exercices

1. Ecrire les méthodes __lt__() (pour lesser than) et __le__() (pour lesser than or equals) permettant de comparer des objets de type Tache suivant leur cle
2. Créer des tâches et les comparer, par exemple:

   
   >>> t1 = Tache("Repas",2)
   >>> t5 = Tache("Courses",6)
   >>> t1 < t5
   True
   
   

3. Ajouter les méthodes __gt()__ et __ge__()

4. Proposer une implémentation d'une file de priorité avec un tableau

   Evaluer le coût d'une insertion dans la file de pririté, et le coût d'une suppression

5. Grâce aux méthodes __lt__(), __le__(), __gt()__ et __ge__() on peut utiliser la classe Tas_max pour faire une file de priorité avec les taches.

   Essayer

   
   t1 = Tache("Repas",2)
   t2 = Tache("Vaisselle",7)
   t3 = Tache("Lessive",5)
   t4 = Tache("Sol",1)
   t5 = Tache("Courses",6)
   
   liste_taches = [t1,t2,t3,t4,t5]
   
   fp  = Tas_max(5)
   fp.cree_tas_max(liste_taches)
   
   print(fp.maximum())
   
   print(fp.supprime_racine())
   
   

6. Une tâche étant dans la file de priorité peut voir sa priorité augmenter

   Proposer une solution à ce problème