Algorithmique

Les bibliothèques matplotlib et numpy

Questions

1. Aller sur le site de matplotlib

2. Copier le code suivant et le coller dans l'éditeur de IDLE

   En cliquant dans le code sur la page de matplotlib comprendre le code ci-dessous

   
   #alias
   import numpy as np
   import matplotlib.pyplot as plt
   
   #l'objet np a une méthode linspace()
   x = np.linspace(0, 1, 100)
   
   #l'objet plt a une méthode plot()
   plt.plot(x, x, label='linéaire')
   plt.plot(x, x**2, label='quadratique')
   plt.plot(x, x**3, label='cubique')
   
   plt.xlabel('x')
   plt.ylabel('y')
   
   plt.title("fonctions de référence")
   
   plt.legend()
   
   plt.show()
   
   

3. Exécuter ensuite le code
4. Modifier le code pour tracer en plus des fonctions données, la fonction inverse sur l'intervalle [0.1,2]

Complexité de la recherche séquentielle d'une valeur dans un tableau

Questions

1. Copier le code suivant et l'exécuter

   Ce code mesure le temps en secondes d'exécution de la fonction est_dans_tableau(val : int,liste : list )->bool

   
   import time
      	
   def est_dans_tableau(val,liste):
       for elt in liste:
      	    if elt == val:
      	        return True
      	return False
      	     
   liste = [i for i in range(1000)]
   t1 = time.time()
   est_dans_tableau(999,liste)
   t2 = time.time()
   print(t2 - t1)
   
   

2. Créer une liste tailles en compréhension de 10000 à 10 millions (suite géométrique de raison 10)
3. Créer une fonction mesurer_temps(tailles) qui retourne une liste contenant les temps d'exécution de la recherche séquentielle de la valeur tailles[i] - 1 dans le tableau de 1 à tailles[i] - 1
4. Ensuite tracer:

   
   tailles = [10**k for k in range(4,8)] 
   plt.plot(tailles,mesurer_temps(tailles))
   plt.show()
       
       

   on obtient cela

   
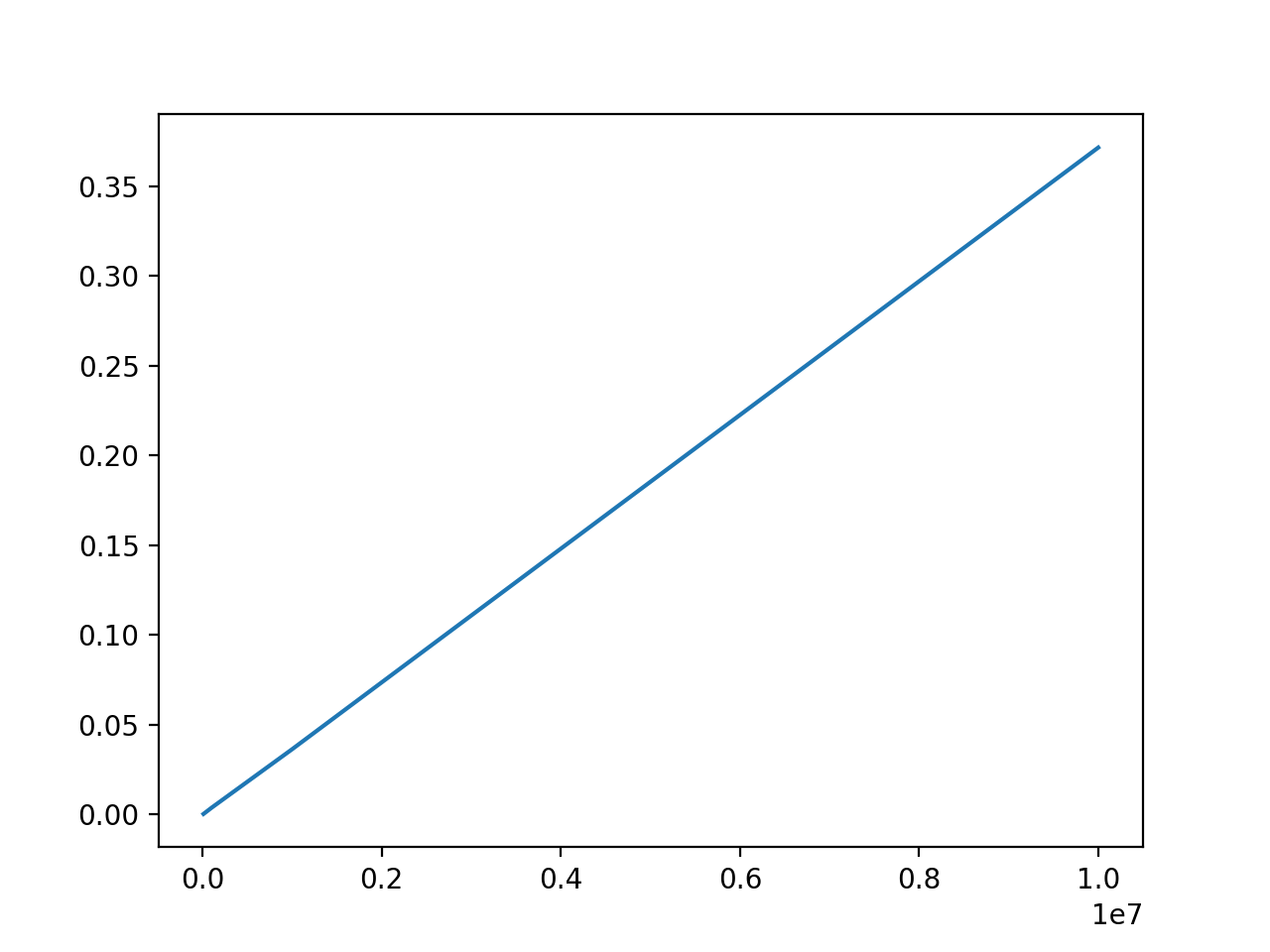
5. Que peut-on dire du temps d'exécution de la recherche séquentielle, dans le pire des cas, en fonction de la taille du tableau?
6. Que peut-on dire du temps d'exécution de la recherche séquentielle, dans le meilleur des cas (lorsque l'élément cherché se trouve en première position du tableau), en fonction de la taille du tableau?

Complexité de la recherche du maximum d'une liste d'entiers

Complexité d'une fonction Python qui trie une liste dans l'ordre croissant

def tri_liste(liste):
"""
trie la liste sur place
"""
	#l'objet liste a une méthode sort()
    liste.sort()