Architecture
Simulation d'une machine de Von Neumann (processeur ARM)
Voir le simulateur ici
A travers plusieurs problèmes il s'agit de comprendre le cycle de fonctionnement du processeur:- Phase de lecture: l'instruction située à l'adresse mémoire fournie par le registre PC est lue et insérée dans le registre CIR
- Phase de décodage et d'exécution: L'unité de contrôle décode l'instruction dans le registre CIR et cette instruction est exécutée souvent avec l'aide de l'unité arithmétique et logique
Problème 1: "Le compte est bon"
- Il s'agit d'obtenir le nombre 84 à partir des nombres 50,25,8,7,3 et 1
avec les opérations : addition et soustraction uniquement
MOV R0,#50 ADD R0,R0,#25 ADD R0,R0,#8 ADD R0,R0,#1 HALT - A vous de jouer : Obtenir 84 à partir de 90,25,8,7,3 et 1 avec les opérations : addition et soustraction uniquement
Problème 2: Multiplier et diviser par 2
- Dans un interpréteur Python exécuter 5 >> 1 puis 5 << 1. Qu'observez vous? (Ecrire 5 en binaire)
- Voir la documentation du simulateur ARM (cliquer sur INFO) et chercher dans le paragraphe The AQA Instruction Set les commandes LSL et LSR
- Traduire en assembleur 5 >> 1 et 5 << 1
- Ecrire une fonction en Python estPair(n) qui retourne vrai si n est pair uniquement avec >> , >> et ==
Problème 3: Le plus grand de deux nombres
- Cliquer sur SELECT et choisir le programme max en assembleur qui affiche le plus grand de deux entiers entrés au clavier le comprendre et l'exécuter (Bien comprendre les instructions B, CMP et BGT voir le manuel )
- Ecrire en assembleur un programme utilisant LSL, LSR, B et BNE qui affiche 1 si le nombre est pair , 0 sinon
- Sauvegarder le programme avec Notepad++ en nommant le fichier avec le suffixe .asm, par exemple estPair.asm
Problème 4: Calculer 1+2+...+n où n est entré au clavier
- Compléter le programme en assembleur ci-dessous pour résoudre le problème puis essayer avec n = 3 en mode pas à pas
- Exécuter avec RUN en vitesse maximale pour n = 10
INP R0,2
MOV R1,#0 // compteur de boucle
MOV R2,#0 // somme
boucle:
ADD ...........
ADD ...........
CMP ...........
.... boucle
OUT R2,4
HALT
Problème 5: Algorithme de la division euclidienne
Etant donné un entier naturel a et un entier naturel b > 0 il existe un unique entier naturel q et un unique entier naturel r tel que a = bq + r avec 0 <= r < b
L'algorithme consiste à retrancher b à a autant de fois que nécessaire jusqu'à ce que le résultat soit strictement inférieur à b
On va utiliser des variables a,b,q et r stockés dans la mémoire après l'instruction HALT
- Compléter le programme en assembleur ci-dessous
- Exécuter
INP R0,2
STR R0,a
INP R1,2
STR R1,b
MOV R2,#0 // q
tantQue:
CMP .......
............
SUB .........
ADD .........
B ...........
fin:
STR R2,q
STR R0,r
HALT
a:0
b:0
q:0
r:0
Problème 6: Algorithme 3N + 1
- Etant donné un entier n > 1, répéter jusqu'à arriver à 1, si le nombre est pair le diviser par 2 sinon multiplier par 3 et ajouter 1
- Ecrire un programme en Python et compter le nombre de nombres visités entre n et 1 exclus
- Ecrire un programme en Assembleur et compter le nombre de nombres visités entre n et 1 exclus
Problème 7: La multiplication égyptienne
Le processeur ARM fait partie de la famille des processeurs RISC (Reduced Instruction Set Computing) ce qui signifie que les instructions du processeur sont en nombre limité.
Nous allons ici programmer en assembleur la multiplication de deux entiers entre eux
Pour calculer le produit P = xy on procède ainsi si x est pair alors P = (x // 2)(2y) sinon P = (x - 1)(y) + y
- Ecrire en Python une fonction multEgyptienne(a,b)
- Ecrire un programme assembleur pour multiplier deux entiers a et b par la méthode égyptienne
Simulation d'une machine de Von Neumann (Partie 2)
Voir le simulateur ici
Nous allons découvrir deux mécanismes intéressants:
- L'adressage indirect: Comment repérer en mémoire ?
- Le mécanisme de la pile
Assembler le code machine (Python)
Ecrire le programme suivant en Python
import dis
dis.dis('x = 2;x = x + 3')
Un programme Python est traduit en langage machine pour être exécuté
Chaque instruction contient un code que le processeur peut décoder ce qui permet ensuite au processeur d'exécuter une tâche bien précise
Avant de voir les codes machines correspondants aux deux instructions précédentes nous allons voir les codes sous forme compréhensible (le langage assembleur)

Pour deux instructions (deux affectations) en assembleur il y a 7 actions
Chaque action par exemple LOAD_CONSTANT a un sens bien précis défini dans la documentation Python

Un élément important, la pile (stack) permet de simplifier la gestion des opérations
Voici comment est effectué l'addition

A partir de ces éléments on peut décoder le code assembleur:
Chaque action a 2 octets, un octet pour le code opératoire (opcode) par exemple LOAD_CONST, puis un octet pour l'adresse mémoire (ou pas)
Si on veut désassembler le code assembleur LOAD_CONST et obtenir le code machine correspondant on utilise le dictionnaire opmap ainsi

Ainsi LOAD_CONST 0 est traduit par 0x64 0x00
Exercice
Finir la traduction
Que donnera en langage assembleur et en langage machine les instructions suivantes ?
x = 2
y = 3
z = x + y
Logisim
Logisim est un logiciel de simulation écrit en Java,qui nous permettra de simuler et tester certaines portes logiques
Lancer Logisim à partir du répertoire isn
Portes logiques élémentaires
Il s'agit d'implémenter les portes Not,And,Or et Xor uniquement avec des portes Nand
Même si ces portes sont déjà à disposition dans logisim , nous allons utiliser la logique des sous-circuits (identique à celle des fonctions) pour créer un sous-circuit pour chacune de ces portes
Not
Not(x) = Nand(x,x)
Selectionner Add Circuit... dans le menu Project et entrer le nom du circuit Nand2Not
Construire le circuit et tester le avec Poke
Cliquer sur A pour pouvoir insérer du texte sur le circuit
Ensuite cliquer sur le pin d'entrée et étiqueter in
Faire de même avec le pin de sortie et étiqueter out
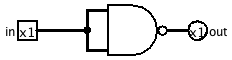
And
And(x,y) = Not(Nand(x,y))
Selectionner Add Circuit... dans le menu Project et entrer le nom du circuit Nand2And
Par glisser-déposer prendre 2 pins d'entrée, un sous-circuit Nand2Not et une porte Nand
Pour cabler Nand2Not on fait glisser la souris au-dessus de la porte pour faire apparaître les étiquettes d'entrée in et de sortie out
Etiqueter les deux entrées in1 et in2 et la sortie out
Construire le circuit

Or
Sachant que Not(Or(x,y)) = And(Not(x),Not(y)), exprimer Or(x,y) uniquement à partir des portes Nand et Not
Créer un nouveau sous-circuit Nand2Or
Xor(ou exclusif)
Sachant que Xor(x,y) = Or(And(Not(x),y),And(x,Not(y))), créer un nouveau sous-circuit Nand2Xor
Portes logiques composites
mux(x,y,sel) = Or(And(Not(sel),x),And(sel,y))
la porte multiplexeur 2:1 permet de faire transiter sur un seul fil deux bits (l'un après l'autre) en fonction de la valeur d'un sélecteur sel
Dmux(in,sel) = (x,y) si sel = 0 alors x = in et y = 0 sinon x = 0 et y = in
Construire un circuit Dmux (démultiplexeur) à partir des portes Not et And
Arithmétique
Additionneur 1 bit
Un additionneur 1 bit est vu comme deux fonctions booléennes s le chiffre des unités et cout la retenue de sortie dépendant de trois entrées
3 entrées : deux bits a et b et une retenue d'entrée cin
2 sorties : Le bit de résultat s et une retenue de sortie cout
Après avoir fait la table de vérité des fonctions s et cout, on obtient comme circuit
Créer un circuit add1 qui implémente l'additionneur 1 bit à partir du schéma ci-dessous

Additionneur 4 bits
En utilisant 4 additionneurs 1 bit créer un additionneur 4 bits- UAL ?
-
Pour trouver l'expression de s puis celle de r_out en fonction de fonctions logiques on va procéder comme en cours et raisonner ainsi
Dans un premier temps supposons r_in égal à 0 à quelle fonction logique vous fait penser s(b1,b2) ?
- Maintenant si r_in est égal à 1 à quelle fonction vous fait penser s(b1,b2) ?
On rappelle que si r_in = 0 alors s = f(b1,b2), si r_in = 1 alors s = g(b1,b2) équivaut à
(r_in and g(b1,b2)) or (not r_in and f(b1,b2))
Donner la décomposition de s
- Procéder de même pour la décomposition de r_out
Nous avons besoin maintenant de coder en Python les fonctions not, and, or, xor prenant des caractères "0" ou "1" en entrée
Tester à l'interpréteur comment se comportent les fonctions natives de Python, not,and et or avec les caractères "0" ou "1"
En déduire les définitions des fonctions
- En déduire la définition de s et de r_out
- En déduire la définition de la fonction add8bits(octet1,octet2)
Additionneur de deux octets
On veut définir une fonction Python add8bits(octet1,octet2) qui additionne deux octets et renvoie un octet, où les octets sont des chaînes de caractères
Regardons sur un exemple de demi-octets

On voit qu'il suffit de définir une fonction add1Bit(bit1,bit2,r_in) qui additionne deux bits avec une retenue en entrée et qui retourne la somme s et aussi une retenue en sortie r_out
Puis répéter cette fonction pour chaque bit
Voici la table de vérité de cette fonction logique
| r_in | b1 | b2 | s | r_out |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Questions
Le temps
Une horloge (clock) délivre un signal périodique par exemple 1 ns (pour une fréquence de 1GHz) . Pour les composants liés à l'horloge (clocked) chaque période compte comme une unité de temps

Lancer Logisim
Réaliser le circuit ci-dessous avec:
- Une horloge (clock) dans Wiring
- Un data flip flop dans Memory
et constater le décalage de la sortie (out) sur l'entrée (in)


Les registres
Nous allons construire un circuit contenant une entrée in(t) (1 bit), un sélecteur load (1 bit) et une sortie out(t) (1 bit) dont le contrat est :
Si load == 1 alors out(t) = in(t-1) sinon out(t) = out(t-1)
C'est le circuit ci-dessous, on utilise un multiplexer pour réaliser le si ...alors

Tester le avec Poke
Ensuite tester le registre à 8 bits fourni par Logisim
Mémoire RAM
Réaliser le circuit suivant simulant une mémoire de 256 octets (vérifier le) .Tester le
Program Counter
Un program counter est un élément du processeur qui à chaque unité de temps t, délivre l'adresse mémoire de la prochaine instruction du programme à exécuter. Il a 4 entrées in, inc, load ,reset, et une sortie.