Types de bases
Documentation d'une fonction en Python
Exercices
On a vu en classe une fonction decToBase(nombre,base) qui affiche à l'écran, du bit de poids faible vers le bit de poids fort, les chiffres de la décomposition de nombre dans la base b
def decToBase(nombre,base): quotient = nombre while quotient != 0: chiffre = quotient % base print(chiffre,end = " ") quotient = quotient // baseA partir de maintenant chaque fonction en Python doit être documentée
Regardons sur un exemple ce que cela signifie
Regardons l'aide de la fonction forward() du module turtle

Regardons maintenant la définition de la fonction forward()

Documentez la fonction decToBase(nombre,base) de la manière suivante
def decToBase(nombre,base): '''paramètres: nombre est un entier naturel écrit en base 10 base est un entier naturel <= 10 résultat: None affiche la conversion de nombre dans la base \ du bit de poids faible vers le bit de poids fort\ de la gauche vers la droite '''Charger la fonction en mémoire (exécutez là avec des valeurs particulières)
Exécuter dans l'interpréteur help(decToBase). Qu'observez vous ?
Codage html de la couleur
le langage html (pour Hyper Text Marked up Language) est le langage qui sert à écrire les pages des sites Web.
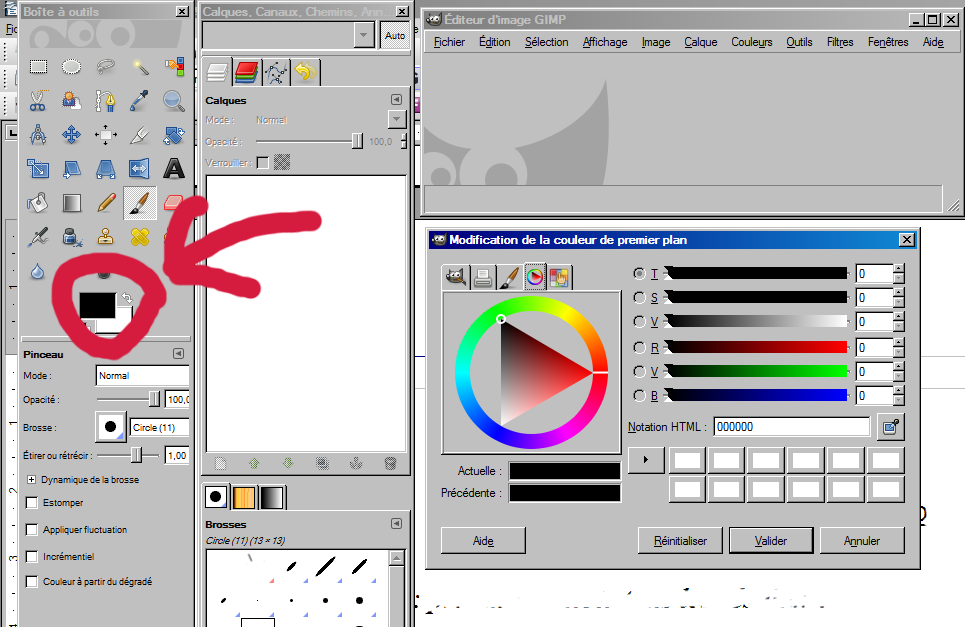
Ouvrir le logiciel Gimp 2.8 (menu démarrer). L'écran devrait comporter trois fenêtres dont une partie est représentée ci-dessus.
Cliquer sur la couleur du texte ou couleur de premier plan (noir normalement). Une nouvelle fenêtre devrait s'ouvrir qui permet de modifier cette couleur.
Elle comporte différentes zones dont : les six réglettes TSV et RVB, la notation HTML, la couleur actuelle (en cours de définition), la couleur précédente (ancienne couleur du texte, noir normalement) et un nuancier cliquable (en haut à gauche) au choix parmi cinq types de nuanciers (présentés par cinq onglets).
Sélectionner le quatrième onglet, celui du cercle TSV. Nous allons à présent en utilisant les réglettes RVB ou leur équivalent numérique à droite, compléter le tableau ci-dessous. Par exemple, la couleur noire est représentée par les trois coordonnées RVB (0;0;0).
Questions
- Nous allons nous concentrer sur le code HTML. À quoi correspondent les deux premiers chiffres de ce code ? Les deux suivants ? Les deux derniers ?
-
Compléter le tableau suivant en vue de décrypter le code HTML, avec les correspondances les plus significatives
Code html RVB Commentaires (0;0;0) (255;0;0) (1;0;0) (10;0;0) (11;0;0) (15;0;0) (16;0;0) (17;0;0) -
A quoi correspondent les lettres a, b, c, d, e, f du code HTML ?
Puis donner le code RVB de abcdef et le code HTML de (232;18;115) et expliquez les.
-
Vous vous êtes peut-être rendu compte que le codage HTML exprime en base 16 les coordonnées RVB.
En base 16 (notation dite hexadécimale),$a_1a_0=a_1\times 16+ a_0$ où les $a_i$ sont les chiffres 0, 1 … 9, a, b, c, d, e, f, ces derniers représentants 10, 11, 12, 13, 14, 15.
Quelle est l'écriture hexadécimale de 234 ? Quelle est l'écriture décimale de ab ?
-
Le chiffre hexadécimal a correspond à 10 en décimal, le chiffre b à 11 en décimal.
Quelle est l'écriture binaire de 10 ? De 11 ? Du nombre codé ab en hexadécimal ?
Par quel moyen simple peut-on passer de l'écriture binaire à l'écriture hexadécimale et réciproquement ?
Conversion avec Python
Pour convertir un nombre décimal en binaire utiliser la fonction bin()
Par exemple bin(7) va retourner la chaîne de caractères '0b111'
Pour convertir un nombre décimal en hexadécimal utiliser la fonction hex()
Par exemple hex(255) va retourner la chaîne de caractères '0xff'
'0x' pour signifier que l'on est dans l'écriture hexadécimale
Questions
Vous devez trouver tout seul comment convertir un nombre en base 16 vers la base 10 à partir d'une documentation fournie
Ouvrir IDLE et dans l'interpréteur Python taper help(int)
Bien que l'aide soit en anglais trouver comment convertir un nombre écrit en base 16, en base 10
- Donner l'écriture hexadécimale de l'octet '0b10111011'
Représentation des entiers négatifs
On aimerait voir comment sont codés les entiers naturels et négatifs "à l'intérieur de la machine"
On va utiliser une fonction de Python qui appliquée à un entier entre parenthèse donne sa représentation en octets, chaque octet codé en hexadécimal
Il s'agit de la fonction .to_bytes(....)
Regardons sur les trois exemples suivants

Dans le premier exemple elle donne le codage sur un octet de -1 on a reconnu 0xff c'est à dire 1111 1111
Dans le deuxième exemple elle donne le codage sur deux octets de -1 et on a que des 1 donc 0xffff c'est à dire 1111 1111 1111 1111
Dans le troisième exemple elle donne le codage de -8 sur 2 octets mais les deux octets cette fois ci ne sont plus identiques donc il faut préciser dans quelle ordre ils doivent être traités, voilà le paramètre byteorder doit être précisé
Il y a deux choix possibles soit byteorder="big" et l'ordre est "de la gauche vers la droite" soit byteorder="little" et l'ordre est "de la droite vers la gauche"
Questions
- En utilisant la fonction to_bytes(....) vérifier les résultats de l'exercice 6, c'est à dire coder sur 2 octets , _1, puis -4, -15
- Donner le codage sur 2 octets de 2019
- Donner le codage sur 2 octets de -2019
- Vérifier à la main
Représentation approximative des réels
Le codage des nombres à virgules suit une norme bien précise la norme IEEE 751 qui n'est pas au programme
Il s'agit seulement de bien comprendre que certains nombres ne sont pas dyadiques et que par conséquent leur représentation en machine étant tronquée cela peut conduire à des calculs faux si on n'y prend pas garde
Voici les premières puissances de 0,5
| (0,5)^n | 0,5 | 0,25 | 0,125 | 0,0625 | 0,03125 | 0,015625 | 0,0078125 | 0,00390125 |
|---|---|---|---|---|---|---|---|---|
| n = | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Questions
- Vérifier que 0,5625 est dyadique
La plus grande puissance de 0,5 contenue dans 0,1 est (0,5)^4 = 0,0625
Compléter 0,1 = (0,5)^4 + reste
Chercher la plus grande puissance de 0,5 contenue dans le reste
En déduire que 0,1 = (0,5)^4 + (0,5)^5 + reste
Continuer et en déduire que 0,1 = (0,5)^4 + (0,5)^5 + (0,5)^8 + (0,5)^9+ reste
En déduire que ce développement est périodique et que 0,1 = 0,1001100110011...... en binaire
Pourquoi la fonction suivante est incorrecte ?
def sontColineaires(xU,yU,xV,yV): return xU*yV - yU*xV == 0- Comment la corriger ?
Codage des caractères (code UNICODE) puis encodage du code Unicode (UTF-8)
Voici une phrase en Grec ancien qui signifie "les animaux courent"
Τἁ ζῷα τρἐχει
Questions
- Faire un clic droit pour faire afficher le code source de la page et vous pouvez voir qu'à chaque caractère est associé un nombre hexadécimal. Quel est le nombre hexadécimal associé à ζ ?
- Voir ici le site de l'organisme qui gère l'Unicode et allez à Greek pour retrouver le nombre hexadécimal qui code ζ
- Sur combien d'octets sera codé ce caractère ?
Va-t-on ensuite juxtaposer les codes Unicode pour coder les chaînes de caractères ?
Lire le document suivant pour répondre à la question précédente

Que retenir ?
-
En Python 3 le type string (chaîne de caractères) est codé en Unicode,à chaque caractère est associé un code, un entier en hexadécimal, par exemple la lettre a a pour code U+61 (en hexadécimal 61), le chiffre 1 a pour code U+31
Ce que l'on nomme Basic Latin est codé de 0x00 à 0x7F (128) et correspond ce qui anciennement s'appelait le code ASCII
D'autres codes: comme é -> 0xE9, œ -> 0x0153 (deux octets),β -> 0x03b1 (deux octets),π -> 0x03C0 , l' équivalent du d en russe la lettre д a pour code en hexadécimal 0x0434
Voici un exemple sur 3 octets 𝔐 -> 0x1D510
En machine il n' y a que des octets, et la transformation du code Unicode en octets, s'appelle l'encodage
L'encodage le plus utilisé de par le monde est à l'heure actuelle l'UTF-8 (pour Unicode Transformation Format) et 8 pour octets
Concrètement si le code du caractère est < 128, l' encodage se fait sur un octet celui du code
Sinon l'encodage donnera une séquence de deux, trois ou quatre octets éventuellement par la transformation suivante:

UTF 8 et fonctions natives de Python
Il s'agit de vérifier à partir de fonctions Python le "hack" de l'utf-8
- Regardons le cas de la lettre Δ dont le code Unicode est U+0394
- En tapant dans l'interpréteur Python s = chr(0x394) le caractère Δ est affecté à s
- Si on veut les octets (bytes) on utilise la commande s.encode() et on obtient deux octets sous la forme b'\xce\x94'
Vérifions que 0xce94 correspond bien à l'encodage utf-8 pour le code de 2 octets 0x394
Convertissons le code Unicode hexadécimal 0x0394 sous la forme de deux octets, on obtient 00000011 10010100 (on fait bin(int(0x0394,16)))
Comment fait on alors pour ne pas se tromper dans l'opération inverse de décodage ?
Pourquoi ne peut on pas se tromper s'il faut décoder 11001110 10010100 01111000 ? Pourquoi on ne peut obtenir que Δx ?
Lorsqu'on lit un octet les premiers bits sont significatifs, on enlève de l'octet les éventuels 1 et le premier zéro, le nombre de 1 obtenus renseigne sur les octets qu'il faudra traiter ensemble, ainsi dans notre exemple 110 signifie qu'il faut traiter les deux octets 11001110 et 10010100 ensemble
Un octet seul commence toujours par 0, si un octet commence par 10, c'est qu'il fait partie d'un groupe de 2, 3 ou 4 octets
Il faut regarder un des octets qui le précédent pour avoir le nombre d'octets du groupe :
110 -> 2 octets, 1110 -> 3 octets, 11110 -> 4 octets
Pour voir si vous avez compris trouver l'encodage en UTF 8 du caractère ζ
On forme le premier octet en ajoutant après la séquence 110 les trois derniers bits de 00000011 et les deux premiers de 10010100, donc on obtient
11001110 qui en hexadécimal est 0xce
Le deuxième octet commence par 10 avec à la suite les bits restants du deuxième octet du code c'est à dire:
10010100 qui en hexadécimal est 0x94
Fonction type()
Une fonction native de Python type() permet de savoir la nature ou le type de l'objet avec lequel on travaille

On voit sur les exemples précédents les trois types de base que l'on a vu , integer (entier), float (nombre à virgule) et string (chaînes de caractères)
Additionneur de deux octets
On veut définir une fonction Python add8bits(octet1,octet2) qui additionne deux octets et renvoie un octet, où les octets sont des chaînes de caractères
Regardons sur un exemple de demi-octets

On voit qu'il suffit de définir une fonction add1Bit(bit1,bit2,r_in) qui additionne deux bits avec une retenue en entrée et qui retourne la somme s et aussi une retenue en sortie r_out
Puis répéter cette fonction pour chaque bit
Voici la table de vérité de cette fonction logique
| r_in | b1 | b2 | s | r_out |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Questions
-
Pour trouver l'expression de s puis celle de r_out en fonction de fonctions logiques on va procéder comme en cours et raisonner ainsi
Dans un premier temps supposons r_in égal à 0 à quelle fonction logique vous fait penser s(b1,b2) ?
- Maintenant si r_in est égal à 1 à quelle fonction vous fait penser s(b1,b2) ?
On rappelle que si r_in = 0 alors s = f(b1,b2), si r_in = 1 alors s = g(b1,b2) équivaut à
(r_in and g(b1,b2)) or (not r_in and f(b1,b2))
Donner la décomposition de s
- Procéder de même pour la décomposition de r_out
Nous avons besoin maintenant de coder en Python les fonctions not, and, or, xor prenant des caractères "0" ou "1" en entrée
Tester à l'interpréteur comment se comportent les fonctions natives de Python, not,and et or avec les caractères "0" ou "1"
En déduire les définitions des fonctions
- En déduire la définition de s et de r_out
- En déduire la définition de la fonction add8bits(octet1,octet2)
Conversion de décimal en une base b <= 10 en utilisant les chaines de caractères
Nous utiliserons très souvent cette année les chaînes de caractères et certaines méthodes (outils) de cette classe
Reprenons par exemple le problème de la représentation d'un nombre dans une base b inférieure ou égale à 10
Questions
Comprendre la concaténation des chaînes de caractères à travers les exemples suivants

- Faire évoluer la fonction decToBase(nombre,base) pour qu'elle retourne une chaîne de caractères, qui représente le nombre dans le bon ordre (Utiliser astucieusement la concaténation afin que la chaîne retournée soit de la gauche vers la droite du bit de poids fort au bit de poids faible)
Utilisation de la bibliothèque doctest et programmation modulaire
On va commencer un fichier Python nommé bases.py que l'on va compléter au fur et à mesure de l'année
Dans ce fichier on définira des fonctions commentées mais aussi avec des exemples d'utilisation
Ces fonctions pourront ensuite être utilisées ailleurs que dans le fichier bases.py
Dans un premier temps on va modifier la fonction decToBase(nombre,base) afin qu'elle retourne une chaîne de caractères
Vous observerez qu'en plus de la documentation on a ajouté des exemples d'appels de la fonction avec le symbole >>>
Attention ! il y a un espace entre >>> et le nom de la fonction
Enregistrer bases.py le charger en mémoire
Ensuite dans l'interpréteur entrez les commandes suivantes

Que s'est il passé ? doctest a exécuté decToBase(4,2) puis a comparé le résultat obtenu avec celui de l'exemple c'est à dire '100' et a refait la même procédure avec decToBase(25,8)
Puisque il n'y a pas de différences il conclut que les test ont réussi
Modifions un des exemples en écrivant decToBase(24,8) à la place de decToBase(25,8)
Relançons le processus de tests et cette fois ci une erreur est détectée
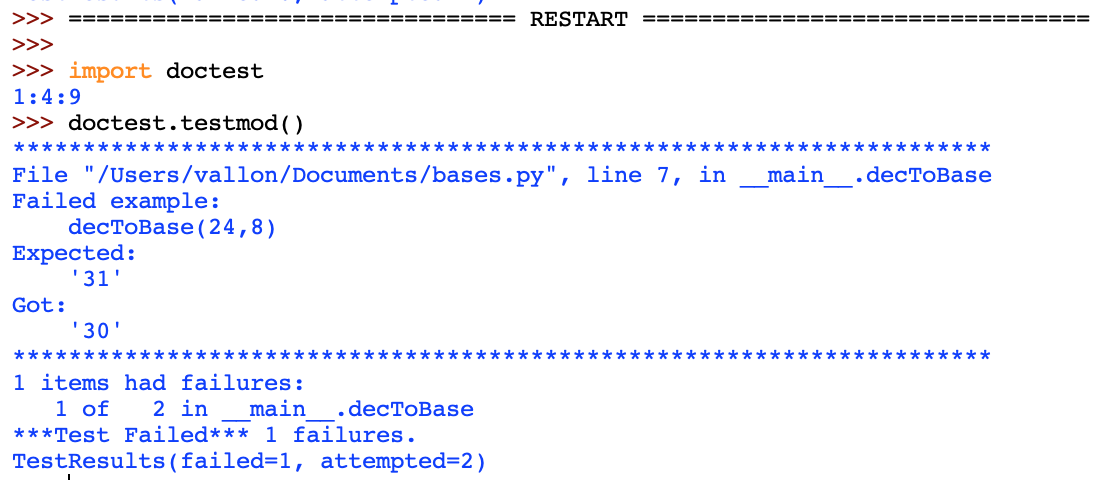
On va rajouter l'importation de doctest et le lancement des tests directement dans bases.py, uniquement si le fichier bases.py n'est pas exécuté à l'extérieur dans un autre fichier .py
Pour cela on rajoute à la fin de bases.py
if __name__ == '__main__': import doctest doctest.testmod()A l'exécution de bases.py vous constatez s'il n'y a pas d'erreurs que doctest est "moins bavard" que précédemment
On va modifier la dernière ligne pour que doctest délivre plus d'informations
if __name__ == '__main__': import doctest doctest.testmod(verbose=True)Voilà à quoi ressemble bases.py pour l'instant
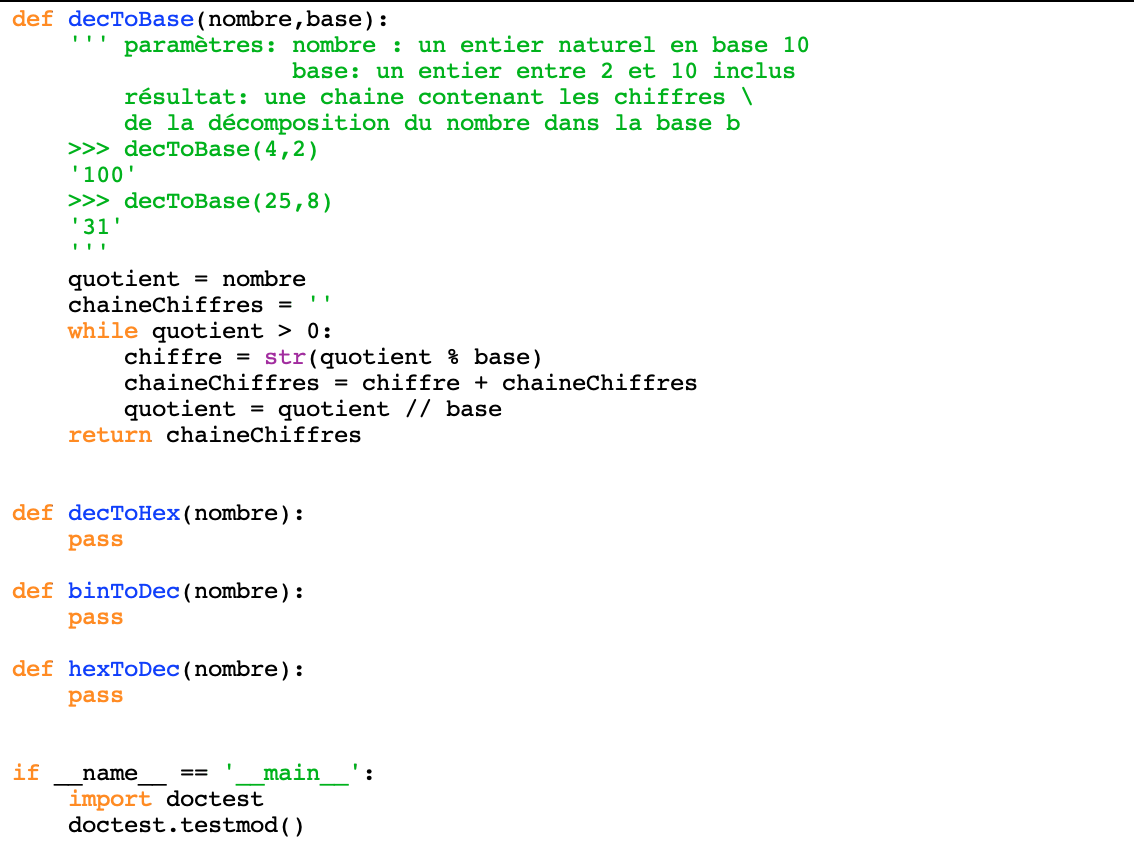
En vous inspirant de ce qui a été fait précédemment
Ecrire la documentation de decToHex(nombre) avec des exemples
Ecrire le corps de la fonction
Relancer les tests pour bases.py
def decToBase(nombre,base):
''' paramètres: nombre : un entier naturel en base 10
base: un entier entre 2 et 10 inclus
résultat: une chaine contenant les chiffres \
de la décomposition du nombre dans la base base
du bit de poids faible vers le bit de poids fort\
de la gauche vers la droite
>>> decToBase(4,2)
'100'
>>> decToBase(25,8)
'31'
'''
quotient = nombre
chaineChiffres = ''
while quotient > 0:
chiffre = str(quotient % base)
chaineChiffres = chiffre + chaineChiffres
quotient = quotient // base
return chaineChiffres